1 người chuyển động thẳng đều với vận tốc V ko đổi từ chân 1 ngọn đèn treo ở độ cao H. Hãy xác định phương chuyển động và độ lớn vận tốc bóng đen do 1 điểm của đỉnh đầu tạo thành biết chiều cao người đó là h

Những câu hỏi liên quan
1 người chuyển động thẳng đều với vận tốc V ko đổi từ chân 1 ngọn đèn treo ở độ cao H. Hãy xác định phương chuyển động và độ lớn vận tốc bóng đen do 1 điểm của đỉnh đầu tạo thành biết chiều cao người đó là
một người có chiều cao h, đứng ngay dưới ngọn đèn treo ở độ cao H (H>h). Người bước đi đều với vận tốc v. Hãy xác định chuyển động của bóng, của đỉnh đầu in lên mặt đất.
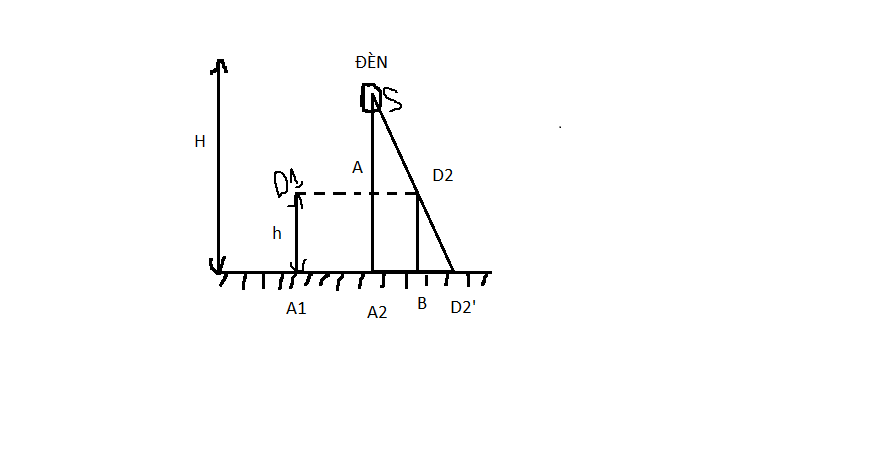
Các tia sáng bị chặn lại bởi người tạo ra một khoảng tối.
\(\Delta D_2BD_2'\)∼ \(\Delta SA_2D_2'\)
\(\Rightarrow\dfrac{BD_2'}{A_2D}=\dfrac{D_2D_2'}{SD_2'}\)
\(\Rightarrow D_2D_2'=SD_2'\cdot\dfrac{BD_2'}{A_2D}=x\cdot\dfrac{h}{H}\)
Xét trong khoảng thời gian t người đó dịch chuyển một đoạn \(S'=C_1C_2=v\cdot t\)
Bóng của đỉnh đầu dịch chuyển một đoạn \(x=C_1D_2'\)
Mà \(x=v\cdot t+x\cdot\dfrac{h}{H}=vt\cdot\dfrac{H}{H-h}\)
\(v'=\dfrac{x}{t}=v\cdot\dfrac{H}{H-h}\)
Đúng 4
Bình luận (1)
Một người có chiều cao h , đứng ngay dưới ngọn đèn treo ở độ cao H(H>h) . người này bước đi đều với vận tốc v . Hãy xác định chuyển động của bóng của đỉnh đầu in trên mặt đât
gọi chân ng đó là A đầu là B bóng của đỉnh đầu là C ta có:
tam giác ABC vuông tại A có AC <AB khi góc BCA >45o
AC =AB khi góc BCA = 45o
AC >AB khi góc BCA <45o
Đúng 0
Bình luận (0)
Một người có chiều cao h,đứng ngay dưới ngọn đèn treo ở độ cao H(H>h).Người này bước đi đều với vận tốc v.Hãy xác định chuyển động của bóng của đỉnh đầu in trên mặt đất
Một người có độ cao h đứng ngay dưới bóng đèn treo ở độ cao H (H>h). Nếu người đó đi đều với vận tốc v. Hãy xác định chuyển động của bóng của đỉnh đầu in trên mặt đất.
Tóm tắt:
Người cao h, đèn cao H (H>h)
Người có vận tốc v, tìm Vbóng =?
Bài làm:
Ta có hình vẽ:
|
Các tia sáng phát ra từ bóng đèn bị người chặn lại tạo ra một khoảng tối trên đất đó là bóng của người đó. Trong khoảng thới gian t, người di chuyển một quảng đường S = BB’ = v.t. Khi đó bóng của đỉnh đầu di chuyển một đoạn đường S’ = BB” Ta có: Δ B " A ' B ' ~ Δ B " S B ⇒ A ' B ' S B = B " B ' B " B ⇒ B " B ' = B " B . A ' B ' S B = x . h H |
||
Mặt khác ta lại có: B”B’= BB’+B’B” ⇔ x= vt+ x . h H ⇒ x = v t . H H − h Vậy vận tốc của bóng của đỉnh đầu là v ' = x t = v H H − h |
|||
Đúng 1
Bình luận (0)
Một người có chiều cao 1,6m đứng ngay dưới ngọn đèn treo ở độ cso 4m. Người này bước đi đều với v=5,4km/h. Hãy xác định tốc độ chuyển động của bóng đỉnh đầu.
Trả lời:
Gọi vận tốc của bóng trên nền nhà là v1
Xét sau một thời gian t
quãng đường mà đỉnh đầu người đi được la s=v*t
quãng đường mà cái bóng trên nền nhà đi được s1=v1*t
vẽ hình ra, từ thời điểm ban đầu đến thời điểm t sẽ tính được tỷ lệ dựa vào định lý talet trong tam giác. ta có kết quả là :
v1= v*H/(H-h)
~Học tốt!~
Một người có độ cao h đứng ngay dưới bóng đèn treo ở độ cao H ( H > h). Nếu người đó đi đều với vận tốc v. Hãy xác định chuyển động của bóng, của đỉnh đầu in trên mặt đất.
Một người có chiều cao h đứng ngay dưới ngọn đèn treo ở độ cao h. Người này bước đi đều với tốc độ v(m/s). Hãy xác định tốc độ chuyển động của bóng đỉnh đầu in trên mặt đất. Áp dụng số: h=1.6cm, H=4m, v=15m/s
Một người có chiều cao h, đừng ngay dưới ngọn đèn treo ở độcao H ( H > h ). Người này bước đi đều với vận tốc v. Hãy xác định chuyển động của bóng của đỉnh đầu in trên mặt đất
Ta có: chiều cao của người đó là AB'
Gọi t là thời gian đi B->B'
v là vận tốc chuyển động trong thời gian t thì BB'=v.t
Gọi quãng đường đi B->B'' là x.
Ta có:
\(\Delta AB'B''\) đồng dạng với \(\Delta SBB''\)
\(\Leftrightarrow \dfrac{AB'}{SB} = \dfrac{B'B"}{BB'' }\)
\(\Leftrightarrow \dfrac{h}{H} = \dfrac{B'B"}{x }
\)
\(\Leftrightarrow B'B" = \dfrac{h.x}{H}\)
BB" = BB' + B'B"
\(\Leftrightarrow x = v.t + \dfrac{h.x}{H}\)
\(\Leftrightarrow Hx = H.v.t + h.x\) ( nhân cả 2 vế cho H)
\(\Leftrightarrow Hx - h.x = H.v.t
\)
\(\Leftrightarrow x( H-h) = H.v.t\)
\(\Leftrightarrow x = \dfrac{H.v.t}{h-x}(*)\)
mà \(v' = \dfrac{BB"}{t}\)
Từ (*). Ta có:
\(v' =\dfrac{BB"}{t} = \dfrac{H.v.t}{h-x} : t = \dfrac{H.v}{H-h}\)
Vậy vận tốc chuyển động của bóng của đỉnh đầu là
Đúng 0
Bình luận (3)
Ta có: chiều cao của người đó là AB'
Gọi t là thời gian đi B->B'
v là vận tốc chuyển động trong thời gian t thì BB'=v.t
Gọi quãng đường đi B->B'' là x.
Ta có:
ΔAB′B′′ΔAB′B″ đồng dạng với ΔSBB′′ΔSBB″
⇔hH=B′B"x⇔hH=B′B"x
⇔x=v.t+h.xH⇔x=v.t+h.xH
⇔Hx=H.v.t+h.x⇔Hx=H.v.t+h.x ( nhân cả 2 vế cho H)
⇔Hx−h.x=H.v.t⇔Hx−h.x=H.v.t
⇔x(H−h)=H.v.t⇔x(H−h)=H.v.t
v′=BB"tv′=BB"t
Từ (*). Ta có:
H.vH−hH.vH−h
Đúng 0
Bình luận (0)


















