Gọi M là điểm bất kì thuộc đường tròn (O) ngoại tiếp tứ giác ABCD. Khoảng cách từ M đến đường thẳng AB, BC, CD, AD theo thứ tự là MH, MK, MI, MN. Chứng minh rằng MH.MI = MK.MN.

Những câu hỏi liên quan
Cho ( O;R ) có dây BC cố định , gọi d là đường thằng qua O và vuông góc với BC ; tiếp tuyến B tại ( O ) cắt đường thẳng d tại A . Gọi M là điểm bất kì thuộc cung nhỏ BC ; từ M kẻ MD , ME , MF theo thứ tự vuông góc với AB , BC , CA tại D , E , Fa . Chứng minh AC là tiếp tuyến ( O;R ) và MDBE , MECF là các tứ giác nội tiếpb . Cho BC Rsqrt{3}. Tính diện tích hình viên phân tạo thành bởi cung nhỏ BC và dây BCc . Chứng minh ME2 MD.MFd . Gọi P là giao điểm của MB và DE , Q là giao điểm của MC và EF...
Đọc tiếp
Cho ( O;R ) có dây BC cố định , gọi d là đường thằng qua O và vuông góc với BC ; tiếp tuyến B tại ( O ) cắt đường thẳng d tại A . Gọi M là điểm bất kì thuộc cung nhỏ BC ; từ M kẻ MD , ME , MF theo thứ tự vuông góc với AB , BC , CA tại D , E , F
a . Chứng minh AC là tiếp tuyến ( O;R ) và MDBE , MECF là các tứ giác nội tiếp
b . Cho BC = R\(\sqrt{3}\). Tính diện tích hình viên phân tạo thành bởi cung nhỏ BC và dây BC
c . Chứng minh ME2 = MD.MF
d . Gọi P là giao điểm của MB và DE , Q là giao điểm của MC và EF . Đường tròn ngoại tiếp tam giác MDP cắt đường tròn ngoại tiếp tam giác MFQ tại điểm thứ hai là N . Chứng minh rằng đường thẳng MN đi qua trung điểm BC
Cho tứ giác ABCD nội tiếp ( O,R). Gọi P, Q lần lượt là giao điểm của AB và CD, AD và BC. Giả sử khoảng cách từ P,Q đến O là p, q. Tính PQ
Hướng dẫn : 2 đường tròn ngoại tiếp tam giác BPC và CQD cắt nhau tại điểm thứ 2 là K. Chứng minh K thuộc PQ. Suy ra PQ=PK+KQ
Bài 1 (4đ). Cho tứ giác ABCD có AB//CD. Gọi M, N lần lượt là trung điểm của AC và BD. Gọi O là giao điểm của hai đường thẳng theo thứ tự đi qua M và N tương ứng vuông góc với BC và AD. a) Chứng minh rằng MN//CD. b) Chứng minh rằng OC OD.
Đọc tiếp
Bài 1 (4đ). Cho tứ giác ABCD có AB//CD. Gọi M, N lần lượt là trung điểm của AC và BD. Gọi O là giao điểm của hai đường thẳng theo thứ tự đi qua M và N tương ứng vuông góc với BC và AD.
a) Chứng minh rằng MN//CD.
b) Chứng minh rằng OC = OD.
Cho đường tròn tâm O đường kính BC, A là một điểm thuộc đường tròn. H là hình chiếu của A trên BC. Vẽ đường tròn (I) có đường kính AH, cắt AB và AC theo thứ tự ở M và N.a) Chứng minh rằng OA vuông góc với MN.b) Vẽ đường kính AOK của đường tròn (O). Gọi E là trung điểm của HK. Chứng minh rằng E là tâm của đường tròn ngoại tiếp tứ giác BMNC.c) Cho BC cố định. Xác định vị trí của điểm A để bán kính của đường tròn ngoại tiếp tứ giác BMNC lớn nhất.
Đọc tiếp
Cho đường tròn tâm O đường kính BC, A là một điểm thuộc đường tròn. H là hình chiếu của A trên BC. Vẽ đường tròn (I) có đường kính AH, cắt AB và AC theo thứ tự ở M và N.
a) Chứng minh rằng OA vuông góc với MN.
b) Vẽ đường kính AOK của đường tròn (O). Gọi E là trung điểm của HK. Chứng minh rằng E là tâm của đường tròn ngoại tiếp tứ giác BMNC.
c) Cho BC cố định. Xác định vị trí của điểm A để bán kính của đường tròn ngoại tiếp tứ giác BMNC lớn nhất.
1)Cho tam giác đều ABC có đường cao AH. Trên cạnh BC lấy M bất kì. Từ M kẻ MP, MQ theo thứ tự vuông góc với AB, AC.
a) tìm tâm O của đường tròn ngoại tiếp tứ giác APMQ
b) CM: OH vuông góc với PQ.
2) Cho hình thang vuông( ^A=D=90o), AB=4cm, BC=13cm, CD= 9cm. Chứng minh rằng đường thẳng AD tiếp xúc với đường tròn có đường kính BC
Cho nửa đường tròn tâm O có đường kính AB. Gọi M là điểm bất kì thuộc nửa đường tròn, H là chân đường vuông góc kẻ từ M đén AB. Vẽ đường tròn (M; MH). Kẻ các tiếp tuyến AC, BD với đường tròn tâm M (C và D là các tiếp điểm khác H). Chứng minh rằng ba điểm C, M, D thẳng hàng và CD là tiếp tuyến của đường tròn (O)
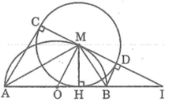
Trong đường tròn (M; MH), theo tính chất hai tiếp tuyến cắt nhau, ta có:
- MA là tia phân giác của góc HMC

Vậy C, M, D thẳng hàng.
Đúng 0
Bình luận (0)
Cho ∆nhọn ABC nội tiếp đường tròn(O) gọi M là giao điểm bất kì trên cung nhỏ BC của đường tròn (O) CM không trùng với BC kẻ MH vuông góc với đường thẳng AB tại H MK vuông góc với đường thẳng AC tại K a.chứng minh tứ giác AHMK nội tiếp b.chứng minh MH.MC=MK.MB
a: góc AHM+góc AKM=90+90=180 độ
=>AHMK là tứ giác nội tiếp
b: Xét ΔMBH vuông tại H và ΔMCK vuông tại K có
góc MBH=góc MCK
=>ΔMBH đồng dạng với ΔMCK
=>MB/MC=MH/MK
=>MB*MK=MC*MH
Đúng 0
Bình luận (0)
Cho đường tròn (O) có hai đường kính AB, CD không vuông góc với nhau.a) Chứng minh: tứ giác ACBD là hình chữ nhật.b) Tiếp tuyến tại A của đường tròn (O) cắt các đường thẳng BC, BD lần lượt tại E, F. Chứng minh: tứ giác ECDF nội tiếp.c) Từ C và D vẽ các tiếp tuyến với đường tròn (O) cắt EF theo thứ tự tại M và N. Chứng minh: MN12EF.d) Gọi I là chân đường vuông góc hạ từ M xuống BN; H là giao điểm của AB và MI. Chứng minh: HA HO.
Đọc tiếp
Cho đường tròn (O) có hai đường kính AB, CD không vuông góc với nhau.
a) Chứng minh: tứ giác ACBD là hình chữ nhật.
b) Tiếp tuyến tại A của đường tròn (O) cắt các đường thẳng BC, BD lần lượt tại E, F. Chứng minh: tứ giác ECDF nội tiếp.
c) Từ C và D vẽ các tiếp tuyến với đường tròn (O) cắt EF theo thứ tự tại M và N. Chứng minh: MN=12EF.
d) Gọi I là chân đường vuông góc hạ từ M xuống BN; H là giao điểm của AB và MI. Chứng minh: HA = HO.
Cho nửa đường tròn O có đường kính AB. Gọi M là điểm bất kì thuộc nửa đường tròn, H là chân đường vuông góc kẻ từ M đến AB. Vẽ đường tròn (M; MH). Kẻ các tiếp tuyến AC, BD với đường tròn tâm M( C và D là các tiếp điểm khác H)
a) Chứng minh rằng ba điểm C, M, D thẳng hàng và CD là tiếp tuyến của đường tròn (O)
b) Chứng minh rằng khi điểm M di chuyển trên nửa đường tròn (O) thì tổng AC + BD không đổi
c) Giả sử CD và AB cắt nhau tại I. Chứng minh rằng tích OH.OI không đổi
Đọc tiếp
Cho nửa đường tròn O có đường kính AB. Gọi M là điểm bất kì thuộc nửa đường tròn, H là chân đường vuông góc kẻ từ M đến AB. Vẽ đường tròn (M; MH). Kẻ các tiếp tuyến AC, BD với đường tròn tâm M( C và D là các tiếp điểm khác H)
a) Chứng minh rằng ba điểm C, M, D thẳng hàng và CD là tiếp tuyến của đường tròn (O)
b) Chứng minh rằng khi điểm M di chuyển trên nửa đường tròn (O) thì tổng AC + BD không đổi
c) Giả sử CD và AB cắt nhau tại I. Chứng minh rằng tích OH.OI không đổi

















