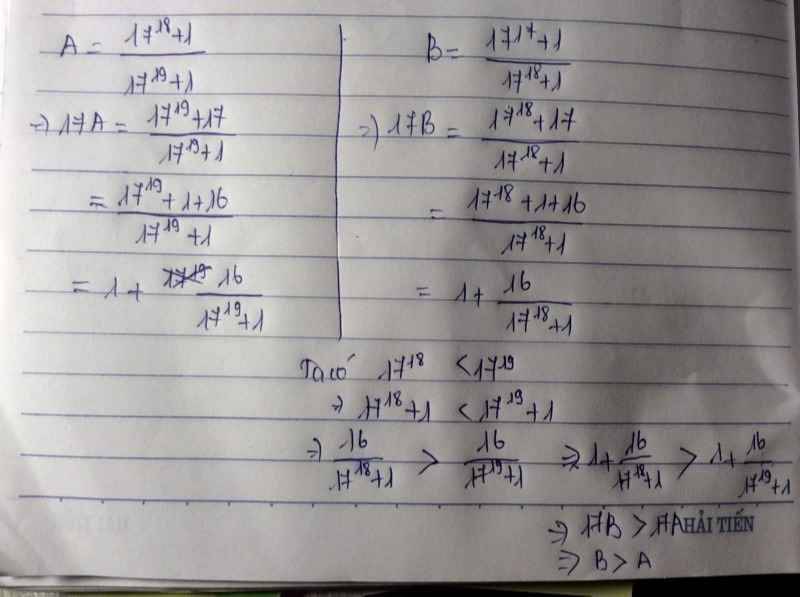So sánh \(\dfrac{-13}{12}\)và \(\dfrac{-19}{18}\)

Những câu hỏi liên quan
So sánh
a)17/20 và 18/19 b)19/18 và 2023/2022
c)13/17 và 135/175 d)53/63 và 535/636
e)13/15 và 22/25 \(\dfrac{2023}{2023^2+1}và\dfrac{2022}{2022^2+1}\)
a) \(\dfrac{17}{20}< \dfrac{18}{20}< \dfrac{18}{19}\Rightarrow\dfrac{17}{20}< \dfrac{18}{19}\)
b) \(\dfrac{19}{18}>\dfrac{19+2024}{18+2024}=\dfrac{2023}{2022}\Rightarrow\dfrac{19}{18}>\dfrac{2023}{2022}\)
c) \(\dfrac{135}{175}=\dfrac{27}{35}\)
\(\dfrac{13}{17}=\dfrac{26}{34}< \dfrac{26+1}{34+1}=\dfrac{27}{35}\)
\(\Rightarrow\dfrac{13}{17}< \dfrac{135}{175}\)
Đúng 4
Bình luận (0)
Cho :
\(S=\dfrac{1}{11}+\dfrac{1}{12}+\dfrac{1}{13}+\dfrac{1}{14}+\dfrac{1}{15}+\dfrac{1}{16}+\dfrac{1}{17}+\dfrac{1}{18}+\dfrac{1}{19}+\dfrac{1}{20}\)
Hãy so sánh S và \(\dfrac{1}{2}\)
Ta có :
\(\dfrac{1}{11}>\dfrac{1}{20}\\ \dfrac{1}{12}>\dfrac{1}{20}\\ ..........\\ \dfrac{1}{20}=\dfrac{1}{20}\)
\(\Rightarrow\dfrac{1}{11}+\dfrac{1}{12}+\dfrac{1}{13}+...+\dfrac{1}{20}>\dfrac{1}{20}+\dfrac{1}{20}+...+\dfrac{1}{20}\\ \Rightarrow S>\dfrac{10}{20}\\ \Rightarrow S>\dfrac{1}{2}\)
Đúng 0
Bình luận (0)
so sánh qua số trung gian:
a)\(\dfrac{12}{49}\);\(\dfrac{13}{47}\)
b)\(\dfrac{12}{47}\);\(\dfrac{19}{77}\)
giúp mk với
a: \(\dfrac{12}{49}< \dfrac{13}{49}< \dfrac{13}{47}\)
b: \(\dfrac{12}{47}>\dfrac{19}{47}>\dfrac{19}{77}\)
Đúng 2
Bình luận (1)
a) Ta chọn phân số \(\dfrac{12}{47}\) là phân số trung gian, ta có :
\(\dfrac{12}{49}< \dfrac{12}{47};\dfrac{13}{47}>\dfrac{12}{47}\Rightarrow\dfrac{12}{49}< \dfrac{13}{47}\)
Đúng 1
Bình luận (0)
Không quy đồng tử số và mẫu số, hãy so sánh các phân số sau
Xem chi tiết
A.\(\dfrac{12}{18}\) và \(\dfrac{13}{17}\) B.\(\dfrac{16}{51}\) và \(\dfrac{31}{90}\)
mik sẽ chỉ tick 4 bn đầu tiên thôi nha
a:
13/17=1-4/17
8/12=1-4/12
mà 4/17<4/12
nên 13/17>8/12=12/18
b: 16/51<17/51=1/3=30/90<31/90
Đúng 2
Bình luận (0)
Hãy so sánh các phân số sau bằng phương pháp so sánh phần bù :
a)\(\dfrac{10}{11}và\dfrac{19}{20}\)
b) \(\dfrac{13}{15}và\dfrac{15}{17}\)
c) \(\dfrac{31}{35}và\dfrac{35}{37}\)
Bài 1:So Sánh(nhanh nhất)
\(\dfrac{-13}{38}va\dfrac{29}{-88},\dfrac{-18}{31}va\dfrac{-1818}{3131}\)
Bài 2:Tính
a)\(\dfrac{-1}{39}+\dfrac{-1}{52}\)
b)\(\dfrac{-6}{9}+\dfrac{-12}{16}\)
Bài 1:
\(\dfrac{-13}{38}\) và \(\dfrac{29}{-88}\)
\(\dfrac{-13}{38}=\dfrac{-13.29}{38.29}=\dfrac{-377}{1102}\)
\(\dfrac{29}{-88}=\dfrac{-29}{88}=\dfrac{-29.13}{88.13}=\dfrac{-377}{1144}\)
Vì \(\dfrac{-377}{1102}< \dfrac{-377}{1144}\) nên \(\dfrac{-13}{38}< \dfrac{29}{-88}\)
\(\dfrac{-18}{31}\) và \(\dfrac{-1818}{3131}\)
\(\dfrac{-18}{31}\)
\(\dfrac{-1818}{3131}=\dfrac{-1818:101}{3131:101}=\dfrac{-18}{31}\)
Vì \(\dfrac{-18}{31}=\dfrac{-18}{31}\) nên \(\dfrac{-18}{31}=\dfrac{-1818}{3131}\)
Đúng 1
Bình luận (0)
Bài 2:
a) \(\dfrac{-1}{39}+\dfrac{-1}{52}=\dfrac{-4}{156}+\dfrac{-3}{156}=\dfrac{-4+-3}{156}=\dfrac{-7}{156}\)
b) \(\dfrac{-6}{9}+\dfrac{-12}{16}=\dfrac{-2}{3}+\dfrac{-3}{4}=\dfrac{-8}{12}+\dfrac{-9}{12}=\dfrac{-17}{12}\)
Đúng 1
Bình luận (0)
So sánh A và B biết:
A=\(\dfrac{17^{18}+1}{17^{19}+1}\) , B=\(\dfrac{17^{17}+1}{17^{18}+1}\)
\(17A=\dfrac{17^{19}+17}{17^{19}+1}=\dfrac{\left(17^{19}+1\right)+16}{17^{19}+1}=\dfrac{17^{19}+1}{17^{19}+1}+\dfrac{16}{17^{19}+1}=1+\dfrac{16}{17^{19}+1}\)
\(17B=\dfrac{17^{18}+17}{17^{18}+1}=\dfrac{\left(17^{18}+1\right)+16}{17^{18}+1}=\dfrac{17^{18}+1}{17^{18}+1}+\dfrac{16}{17^{18}+1}=1+\dfrac{16}{17^{18}+1}\)
Vì \(17^{19}>17^{18}=>17^{19}+1>17^{18}+1\)
\(=>\dfrac{16}{17^{19}+1}< \dfrac{16}{17^{18}+1}\)
\(=>17A< 17B=>A< B\)
Đúng 1
Bình luận (0)
So sánh:
\(\dfrac{13}{19};\dfrac{47}{53}\)
\(1-\dfrac{13}{19}=\dfrac{6}{19}\\ 1-\dfrac{47}{53}=\dfrac{6}{53}\\ \dfrac{6}{19}>\dfrac{6}{53}\Rightarrow\dfrac{13}{19}< \dfrac{47}{53}\)
Đúng 3
Bình luận (1)
so sánh 2 phân số \(\dfrac{13}{24}\)và \(\dfrac{12}{14}\)
ta có : `12/14 = 6/7`
`13/24=(13xx7)/(24xx7)= 91/168`
`6/7=(6xx24)/(7xx24)= 144/168`
mà : `91<144`
`=> 13/24 < 12/14`
Đúng 2
Bình luận (0)
\(\dfrac{13}{24}\) = \(\dfrac{13\times7}{24\times7}\) = \(\dfrac{91}{168}\)
\(\dfrac{12}{14}\) = \(\dfrac{12\times12}{14\times12}\) = \(\dfrac{144}{168}\)
\(\dfrac{91}{689}< \dfrac{144}{168}\)
\(\dfrac{13}{24}\) < \(\dfrac{12}{14}\)
Đúng 2
Bình luận (0)