Tính chu vi của đường tròn ngoại tiếp và diện tích của hình tròn nội tiếp hình vuông có cạnh 20 cm

Những câu hỏi liên quan
Tính chu vi của đường tròn ngoại tiếp và diện tích của hình tròn nội tiếp hình vuông có cạnh 20 cm
Cho hình vuông ABCD có diện tích 36 cm Vuông chu vi của hình tròn ngoại tiếp hình vuông ABCD bằng
S ABCD=36cm2
=>\(AB=\sqrt{36}=6\left(cm\right)\)
\(AC=\sqrt{6^2+6^2}=6\sqrt{2}\left(cm\right)\)
=>\(R=\dfrac{6\sqrt{2}}{2}=3\sqrt{2}\left(cm\right)\)
\(S=R^2\cdot3.14=18\cdot3.14=56.52\left(cm^2\right)\)
Đúng 0
Bình luận (0)
a) Vẽ hình vuông cạnh 4 cm.
b) Vẽ đường tròn ngoại tiếp hình vuông đó. Tính bán kinh R của đường tròn này.
c) Vẽ đường tròn nội tiếp hình vuông đó. Tính bán kính r của đường tròn này.
a) Vẽ hình vuông cạnh 4cm.
b) Vẽ đường tròn ngoại tiếp hình vuông đó. Tính bán kính R của đường tròn này.
c) Vẽ đường tròn nội tiếp hình vuông đó. Tính bán kính r của đường tròn này.
Hướng dẫn trả lời:
a) Dùng êke ta vẽ hình vuông ABCD có cạnh bằng 4cm như sau:
- Vẽ AB = 4cm.
- Vẽ BC ⊥ AB và BC = 4cm
- Vẽ DC ⊥ BC và DC = 4cm
- Nối D với A, ta có AD ⊥ DC và AD = 4cm
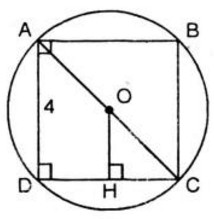
b) Tam giác ABC là tam giác vuông cân nên AB = BC.
Áp dụng định lí Py – ta – go trong tam giác vuông ABC, ta có:
AC2=AB2+BC2=2AB2⇔AC2=2.42=32⇒AC=√32=4√2AC2=AB2+BC2=2AB2⇔AC2=2.42=32⇒AC=32=42
Vậy AO=R=AC2=4√22=2√2AO=R=AC2=422=22
Vậy R = 2√2 cm
c) Vẽ OH ⊥ Dc. Vẽ đường tròn tâm O, bán kính OH. Đó là đường tròn nội tiếp hình vuông ABCD
Ta có: OH=AD2=2(cm)OH=AD2=2(cm)
Vậy r = OH = 2cm
\
Đúng 0
Bình luận (0)
Hình Vuông ABCD có cạnh 2 cm . Tính bán kính đường tròn ngoại tiếp , nội tiếp hình vuông ABCD
AC=căn 2^2+2^2=2*căn 2(cm)
=>R=căn 2(cm)
S1=R^2*3,14=6,28cm2
r=AB/2=1cm
S2=1^2*3,14=3,14cm2
Đúng 0
Bình luận (0)
Viết chương trình con:
a) Tính chu vi và diện tích hình tròn theo bán kính.
b) Tính diện tích tam giác, bán kính đường tròn nội và ngoại tiếp tam giác theo 3 cạnh.
c) Tính thể tích và đường chéo hình hộp chữ nhật theo 3 kích thước.
Một đường tròn nội tiếp trong một hình vuông có cạnh bằng 5 . Sau đó nội tiếp trong hình vuông đó một hình tròn và quá trình đó cứ tiếp diễn như thế mãi. Nếu gọi Sn là tổng các diện tích của n hình tròn đầu tiên nội tiếp như thế. Tính S20.
Chân thành cảm ơn và hậu tạ.
a) Vẽ hình vuông cạnh 4cm.
b) Vẽ đường tròn ngoại tiếp hình vuông đó. Tính bán kính R của đường tròn này.
c) Vẽ đường tròn nội tiếp hình vuông đó. Tính bán kính r của đường tròn này.
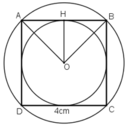
a) Vẽ hình vuông ABCD có cạnh 4cm.
b) Vẽ hai đường chéo AC và BD. Chúng cắt nhau tại O.
Đường tròn (O; OA) là đường tròn ngoại tiếp hình vuông ABCD.
Ta có:
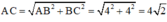 (cm)
(cm)
⇒ R = OA = AC/2 = 2√2 (cm).
c) Gọi H là trung điểm AB.
(O ; OH) là đường tròn nội tiếp hình vuông ABCD.
r = OH = AD/2 = 2cm.
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A. Trên cạnh AC lấy điểm M. Vẽ đường tròn đường kính MC. Kẻ BM cắt đường tròn tại D. Đường thẳng DA cắt đường tròn tại S. Chứng minh rằng :
a) Tứ giác ABCD nội tiếp được đường tròn
b) Góc ACB = góc ACS
c) Tính diện tích và chu vi của đường tròn ngoại tiếp tứ giác ABCD, biết AB= 9cm, AC= 12 cm
trong hình bên: hình vuông có diện tích 81cm2. vậy chu vi của hình tròn là : biết hình tròn nội tiếp hình vuông
Cạnh hình vuông = 9cm
Chu vi hình tròn là 9x3.14=28.26cm
_Kudo_














