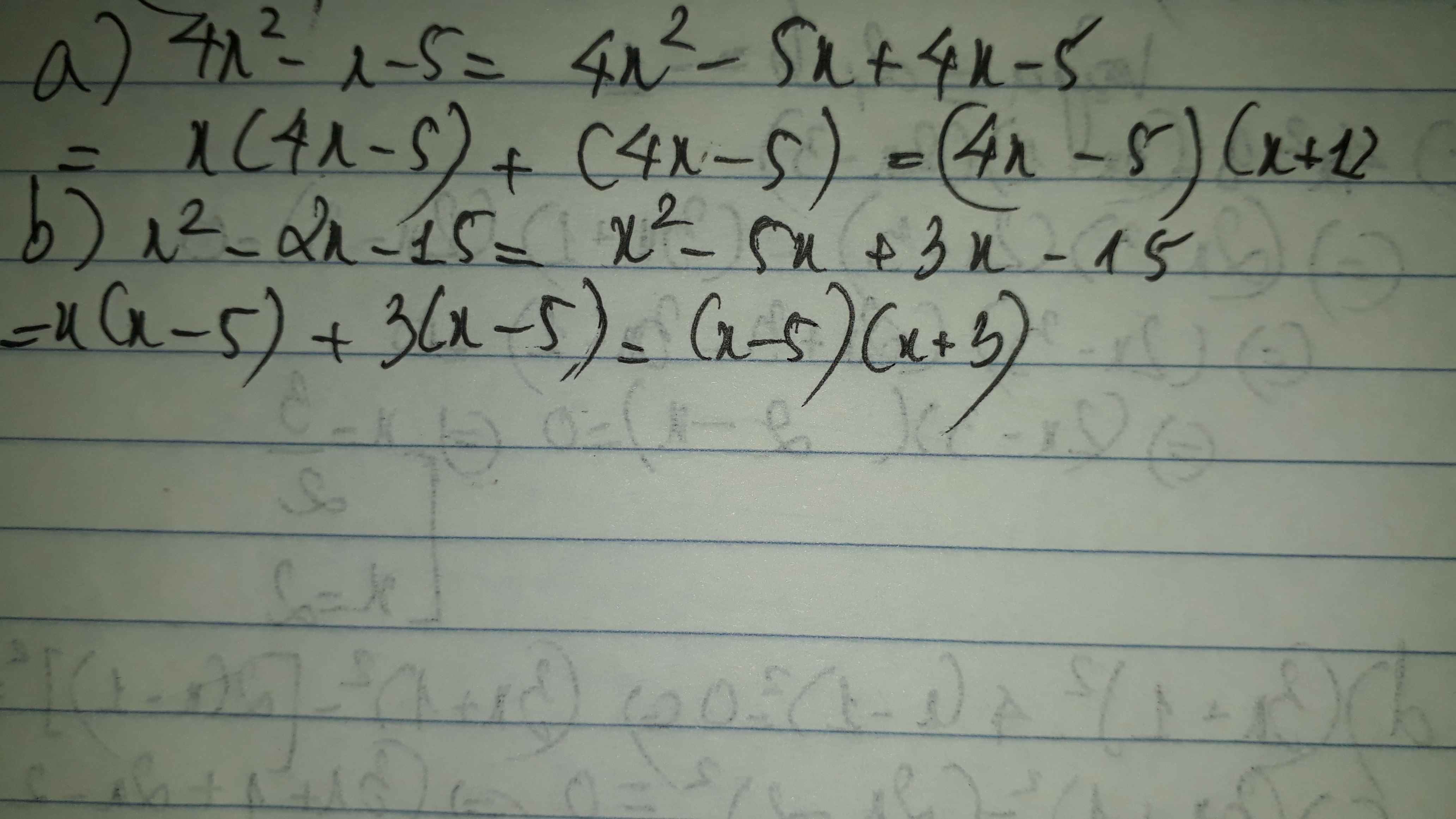= [x² - 2.x.\(\frac{11}{2}\) + \(\left(\frac{11}{2}\right)^2\)] - \(\frac{121}{4}\)+ 8 = (x - \(\frac{11}{2}\))² - \(\frac{89}{4}\) =  (x - \(\frac{11}{2}\))² - \(\left(\frac{\sqrt{89}}{2}\right)^2\)

= \(\left(x-\frac{11}{2}-\frac{\sqrt{89}}{2}\right).\left(x-\frac{11}{2}+\frac{\sqrt{89}}{2}\right)\)= \(\left(x-\frac{11+\sqrt{89}}{2}\right).\left(x+\frac{\sqrt{89}-11}{2}\right)\)

phương pháp này mình gọi là phương pháp nhẩm nghiệm:

- Nếu tổng tất cả các hệ số bằng o thì đa thức có 1 nghiệm là x=1 hay chứa thừa số là x-1

- Nếu tổng tất cả các hệ số bậc chẵn bằng tổng các hệ số bậc lẻ thì đa thức có một nghiệm là x=-1 hay chứa thừa số là x+1

a) \(x^3+4x^2-21x\)

\(=x\left(x^2+4x-21\right)\)

\(=x\left(x^2-3x+7x-21\right)\)

\(=x\left[x\left(x-3\right)+7\left(x-3\right)\right]\)

\(=x\left(x-3\right)\left(x+7\right)\)

b) \(5x^3+6x^2+x\)

\(=x\left(5x^2+6x+1\right)\)

\(=x\left(5x^2+5x+x+1\right)\)

\(=x\left[5x\left(x+1\right)+\left(x+1\right)\right]\)

\(=x\left(x+1\right)\left(5x+1\right)\)

c) \(x^3-7x+6\)

\(=x^3+2x^2-3x-2x^2-4x+6\)

\(=x\left(x^2+2x-3\right)-2\left(x^2+2x-3\right)\)

\(=\left(x-2\right)\left(x^2+2x-3\right)\)

\(=\left(x-2\right)\left(x-1\right)\left(x+3\right)\)

d) \(3x^3+2x-5\)

\(=3x^3+3x^2+5x-3x^2-3x-5\)

\(=x\left(3x^2+3x+5\right)-\left(3x^2+3x+5\right)\)

\(=\left(x-1\right)\left(3x^2+3x+5\right)\)

a: \(4x^2-x-5=\left(4x-5\right)\left(x+1\right)\)

b: \(x^2-2x-15=\left(x-5\right)\left(x+3\right)\)

Lời nói chẳng mất tiền mua. Lựa lời mà chửi cho vừa lòng nhau. Đã chửi, phải chửi thật đau. Chửi mà hiền quá còn lâu nó chừa. Chửi đúng , không được chửi bừa . Chửi cha mẹ nó , không thừa một ai . Khi chửi , chửi lớn mới oai. Chửi hay là phải chửi dài , chửi lâu . Chửi đi chửi lại mới ngầu. Chửi nhiều cho nó nhức đầu , đau tai. Chửi xong nhớ nói bái bai . Phóng nhanh kẻo bị ăn chai vào mồm. 

\(a,9x^2+6x-8\)

\(=\left(3x\right)^2+2.3x+1-9\)

\(=\left(3x+1\right)^2-3^3\)

\(=\left(3x+1-3\right)\left(3x+1+3\right)=\left(3x-2\right)\left(3x+4\right)\)

\(b,4x^2-4x-3\)

\(=\left(2x\right)^2-2.2x+1-4\)

\(=\left(2x-1\right)^2-2^2\)

\(=\left(2x-1-2\right)\left(2x-1+2\right)=\left(2x-3\right)\left(2x+1\right)\)

Cảm ơn bạn

ấn máy tính để tìm nghiệm rồi phân tích ra

\(x^3-4x^2+4x-1\)

\(=x^3-x^2-3x^2+3x+x-1\)

\(=x^2\left(x-1\right)-3x\left(x-1\right)+\left(x-1\right)\)

\(=\left(x-1\right)\left(x^2-3x+1\right)\)

này đinh đức hùng không phân tích nữa à , cái đằng sau còn phân tích được nữa đấy

a. \(=4x^3-12x^2-x^2+3x+6x-18=\left(x-3\right)\left(4x^2-x+6\right)\)

b.  \(=-x^3+x^2-7x^2+7x-x+1=\left(x-1\right)\left(-x^2-7x-1\right)\)

c.  \(=x^3+2x^2-6x^2-12x+4x+8=\left(x+2\right)\left(x^2-6x+4\right)\)

x²-10x+16=x²-8x-2x+16=(x²-8x)-(2x-16)=x(x-8)-2(x-8)=(x-8)(x-2)

Đa thức này không phân tích được đâu bạn