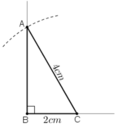
Dựng tam giác ABC vuông tại B, biết cạnh huyền AC = 4cm, cạnh góc vuông BC = 2cm.

Những câu hỏi liên quan
Dựng tam giác ABC vuông tại B, biết cạnh huyền AC = 4cm, cạnh góc vuông BC = 2cm.
a) Phân tích:
Giả sử dựng được ΔABC thỏa mãn yêu cầu.
Ta dựng được đoạn BC vì biết BC = 2cm.
Khi đó điểm A là giao điểm của:
+ Tia Bx vuông góc với BC
+ Cung tròn tâm C bán kính 4cm.
b) Cách dựng:
+ Dựng đoạn thẳng BC = 2cm.
+ Dựng tia Bx vuông góc với cạnh BC.
+ Dựng cung tròn tâm C, bán kính 4cm. Cung tròn cắt tia Bx tại A.
Kẻ AC ta được ΔABC cần dựng.
c) Chứng minh
ΔABC có góc B = 90º, BC = 2cm.
A thuộc cung tròn tâm C bán kính 4cm nên AC = 4cm.
Vậy ΔABC thỏa mãn yêu cầu đề bài
d) Biện luận: Ta luôn dựng được một hình thang thỏa mãn điều kiện của đề bài.
Đúng 0
Bình luận (0)
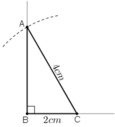
Dựng tam giác ABC vuông tại B, biết cạnh huyền AC = 4cm, cạnh góc vuông BC = 2cm.
a) Phân tích:
Giả sử dựng được ΔABC thỏa mãn yêu cầu.
Ta dựng được đoạn BC vì biết BC = 2cm.
Khi đó điểm A là giao điểm của:
+ Tia Bx vuông góc với BC
+ Cung tròn tâm C bán kính 4cm.
b) Cách dựng:
+ Dựng đoạn thẳng BC = 2cm.
+ Dựng tia Bx vuông góc với cạnh BC.
+ Dựng cung tròn tâm C, bán kính 4cm. Cung tròn cắt tia Bx tại A.
Kẻ AC ta được ΔABC cần dựng.
c) Chứng minh
ΔABC có góc B = 90º, BC = 2cm.
A thuộc cung tròn tâm C bán kính 4cm nên AC = 4cm.
Vậy ΔABC thỏa mãn yêu cầu đề bài
d) Biện luận: Ta luôn dựng được một hình thang thỏa mãn điều kiện của đề bài.
Đúng 0
Bình luận (0)
Dựng tam giác ABC vuông tại B, biết cạnh huyền AC = 4m, cạnh góc vuông BC = 2cm
Bài giải:
Sử dụng phương pháp dựng phương pháp vuông đã được học.
Ta lần lượt thực hiện:
- Vẽ góc vuông xBy. Trên tia Bx lấy điểm C sao cho BC = 2cm.
- Vẽ đường tròn (C; 4) và đường tròn này cắt tia Oy tại A.
Nối A với C ta được ∆ABC là tam giác cần dựng.
Đúng 0
Bình luận (0)
Dựng tam giác ABC vuông tại A, biết cạnh huyền BC = 4,5cm và cạnh góc vuông AC = 2cm
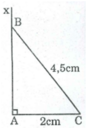
Cách dựng:
- Dựng đoạn AC = 2cm.
- Dựng góc ∠ (CAx) bằng 90 0
- Dựng cung tròn tâm C bán kính 4,5cm cắt Ax tại B. Nối CB ta có ΔABC cần dựng .
Chứng minh:
∆ ABC có ∠ A = 90 0 , AC = 2 cm, BC = 4,5 cm.
Thỏa mãn điều kiện bài toán.
Đúng 0
Bình luận (0)
Dựng tam giác ABC vuông tại A, biết cạnh huyền BC = 4,5cm và cạnh góc vuông AC = 2cm ?
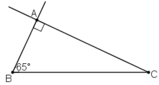
Dựng tam giác ABC vuông tại A, biết cạnh huyền BC = 4cm, góc nhọn B = 65o.
a) Phân tích
Giả sử dựng được ΔABC thỏa mãn yêu cầu đề bài.
Đoạn thẳng BC dựng được vì đã biết độ dài.
Khi đó điểm A là giao điểm của:
+ Tia Bx tạo với đoạn thẳng BC góc 65º
+ Đường thẳng qua C và vuông góc với tia Bx vừa dựng.
b) Cách dựng:
- Dựng đoạn thẳng BC = 4cm.
- Dựng tia Bx tạo với BC một góc 65º.
- Dựng đường thẳng a qua C và vuông góc với Bx.
- Bx cắt a tại A.
ΔABC là tam giác cần dựng.
c) Chứng minh: ΔABC vừa dựng vuông tại A, góc B = 65º và BC = 4cm.
d) Biện luận: Ta luôn dựng được một tam giác thỏa mãn điều kiện đề bài.
Đúng 0
Bình luận (0)
Dựng tam giác ABC vuông tại A, biết cạnh huyền BC = 4cm, góc nhọn B = 65o.
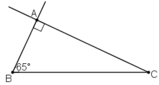
a) Phân tích
Giả sử dựng được ΔABC thỏa mãn yêu cầu đề bài.
Đoạn thẳng BC dựng được vì đã biết độ dài.
Khi đó điểm A là giao điểm của:
+ Tia Bx tạo với đoạn thẳng BC góc 65º
+ Đường thẳng qua C và vuông góc với tia Bx vừa dựng.
b) Cách dựng:
- Dựng đoạn thẳng BC = 4cm.
- Dựng tia Bx tạo với BC một góc 65º.
- Dựng đường thẳng a qua C và vuông góc với Bx.
- Bx cắt a tại A.
ΔABC là tam giác cần dựng.
c) Chứng minh: ΔABC vừa dựng vuông tại A, góc B = 65º và BC = 4cm.
d) Biện luận: Ta luôn dựng được một tam giác thỏa mãn điều kiện đề bài.
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A đường cao AH. Chia cạnh huyền BC thành 2 đoạn thẳng HB=1cm và HC=4cm. Dựng đường tròn (A;2cm) A. Tính Ah,AB,AC và các góc B, góc C của tam giác ABC B. Chứng minh BC là tiếp tuyến đường tròn (A;2cm) C. Dựng đường kính DH của đường tròn (A;2cm). Tiếp tuyến của đường tròn (A;2cm) tại D cắt tia đối của tia AB ở E. Chứng minh tứ giác BDRH là hình bình hành.
a: Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\)
=>\(AH^2=1\cdot4=4\)
=>\(AH=\sqrt{4}=2\left(cm\right)\)
BC=BH+CH
=>BC=1+4=5(cm)
XétΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot CB\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}AB^2=1\cdot5=5\\AC^2=4\cdot5=20\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}AB=\sqrt{5}\left(cm\right)\\AC=2\sqrt{5}\left(cm\right)\end{matrix}\right.\)
Xét ΔABC vuông tại A có \(sinC=\dfrac{AB}{BC}=\dfrac{\sqrt{5}}{5}\)
nên \(\widehat{C}\simeq27^0\)
ΔABC vuông tại A
=>\(\widehat{B}+\widehat{C}=90^0\)
=>\(\widehat{B}=90^0-27^0=63^0\)
b: AH=2cm
=>H thuộc (A;2cm)
Xét (A;2cm) có
AH là bán kính
BC\(\perp\)AH tại H
Do đó: BC là tiếp tuyến của (A;2cm)
c: Sửa đề: BDEH
Xét ΔAHB vuông tại H và ΔADE vuông tại D có
AH=AD
\(\widehat{HAB}=\widehat{DAE}\)
Do đó: ΔAHB=ΔADE
=>HB=DE
Xét tứ giác BDEH có
BH//ED
BH=ED
Do đó: BDEH là hình bình hành
Đúng 0
Bình luận (0)
Dựng tam giác ABC vuông tại A, biết cạnh huyền BC = 4cm, góc nhọn \(\widehat{B}=65^0\)
Bài giải:
Sử dụng phương pháp dựng tam giác vuông đã được học.
Ta lần lượt thực hiên:
- Vẽ đoạn BC = 4cm.
- Vẽ tia Bx tạo với BC một góc 650
- Vẽ đường thẳng a qua C và vuông góc với Bx và cắt Bx tại A.
Khi đó ∆ABC là tam giác cần dựng.
Đúng 0
Bình luận (0)











