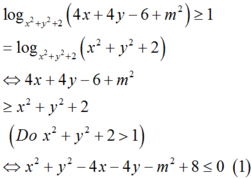
Ta có

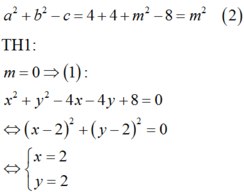
Cặp số x ; y = 2 ; 2  không thỏa mãn điều kiện .

Tập hợp các cặp số (x;y) thỏa mãn (1) là hình tròn  C1(kể cả biên) tâm I1(2;2) bán kính R 1 = m .

Tập hợp các cặp số (x;y) thỏa mãn (2) là đường tròn C2 tâm I 2 - 1 ; 2  bán kính R 2 = 1 + 4 - 1 = 2 .

Để tồn tại duy nhất cặp số (x;y)  thỏa mãn 2 điều kiện (1)  và (2) Xảy ra 2 trường hợp sau:

TH1: C1;  C2tiếp xúc ngoài 

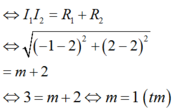
TH2: C1; C2 tiếp xúc trong và

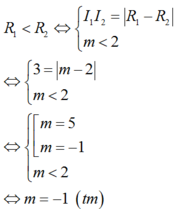
Vậy  S = - 1 ; 1 .

Chọn D.

từ phương trình số 2 ta có 
\(\left(x+y\right)\left(x+2y\right)+\left(x+y\right)=0\Leftrightarrow\left(x+y\right)\left(x+2y+1\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}x+y=0\\x+2y+1=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=-y\\x=-2y-1\end{cases}}\)

lần lượt thay vào 1 ta có 

\(\orbr{\begin{cases}y^2+7=y^2+4y\\\left(-2y-1\right)^2+7=y^2+4y\end{cases}\Leftrightarrow\orbr{\begin{cases}y=\frac{7}{4}\\3y^2+8=0\end{cases}}}\)

vậy hệ có nghiệm duy nhất \(x=-y=-\frac{7}{4}\)

+ 2x2 + y2 – 8x + 2y – 1 = 0 không phải phương trình đường tròn vì hệ số của x2 khác hệ số của y2.

+ Phương trình x2 + y2 + 2x – 4y – 4 = 0 có :

a = –1; b = 2; c = –4 ⇒ a2 + b2 – c = 9 > 0

⇒ phương trình trên là phương trình đường tròn.

+ Phương trình x2 + y2 – 2x – 6y + 20 = 0 có :

a = 1; b = 3; c = 20 ⇒ a2 + b2 – c = –10 < 0

⇒ phương trình trên không là phương trình đường tròn.

+ Phương trình x2 + y2 + 6x + 2y + 10 = 0 có :

a = –3; b = –1; c = 10 ⇒ a2 + b2 – c = 0 = 0

⇒ phương trình trên không là phương trình đường tròn.

\(\Leftrightarrow5\left(x^4+2x^2+1\right)+2\left(y^6+2y^3+1\right)=13\)

\(\Leftrightarrow5\left(x^2+1\right)^2+2\left(y^3+1\right)^2=13\)

\(\Leftrightarrow\left(x^2+1\right)^2=\dfrac{13-2\left(y^3+1\right)^2}{5}\le\dfrac{13}{5}< 4\)

\(\Rightarrow x^2+1< 2\Rightarrow x^2< 1\)

\(\Leftrightarrow x=0\)

\(\Rightarrow y^6+2y^3-3=0\Rightarrow\left[{}\begin{matrix}y^3=1\Rightarrow y=1\\y^3=-3\left(ktm\right)\end{matrix}\right.\)

Vậy \(\left(x;y\right)=\left(0;1\right)\)