x là số tự nhiên
48 là tổng của x bình phương với 2
Vậy x bằng mấy

Những câu hỏi liên quan
Mọi người giúp đỡ mình với.
Câu 1:Tìm 4 số tự nhiên biết tổng nghịch đảo của chúng bằng 1
Câu 2:Tìm 4 số tự nhiên biết tổng bình phương của chúng bằng 1
Câu 3:Tìm p để 4p+1 là số chính phương
Câu 4:Tìm số nguyên dương để x2 +x +6 là số chính phương
Cho biết phương trình
log
9
x
+
log
9
x
+
4
26 có nghiệm dạng
x
3
n
, với n là số tự nhiên. Tổng tất cả các chữ số của bằng A. 9 B. 5 C. 6 D. 3
Đọc tiếp
Cho biết phương trình log 9 x + log 9 x + 4 = 26 có nghiệm dạng x = 3 n , với n là số tự nhiên. Tổng tất cả các chữ số của bằng
A. 9
B. 5
C. 6
D. 3
Chọn C
log
9
x
+
log
9
x
+
4
= 26 (1) 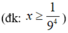
Đặt ![]()
![]()
Phương trình (1) trở thành: ![]()
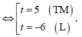
Với t = 5 ![]() (thỏa mãn) => n = 42
(thỏa mãn) => n = 42
Vậy tổng tất cả các chữ số của n là 4 + 2 = 6
Đúng 0
Bình luận (0)
Cho x, y là các số tự nhiên thỏa mãn \(3y^2+1=4x^2\). Chứng minh rằng x là tổng bình phương của hai số tự nhiên liên tiếp.
Cho x;y là các số tự nhiên thỏa mãn \(3y^2+1=4x^2\). Chứng minh rằng x là tổng bình phương của hai số tự nhiên liên tiếp
Ta có : \(3y^2+1=4x^2\)
\(\Leftrightarrow3y^2=4x^2-1\)
\(\Leftrightarrow3y^2=\left(2x+1\right)\left(2x-1\right)\)
Mà : \(2x+1\) và \(2x-1\) nguyên tố cùng nhau
\(\Rightarrow\hept{\begin{cases}2x-1=3m^2\\2x+1=n^2\end{cases}}\) hoặc \(\Rightarrow\hept{\begin{cases}2x-1=m^2\\2x+1=3n^2\end{cases}}\)
TH 1 : \(\hept{\begin{cases}2x-1=3m^2\\2x+1=n^2\end{cases}}\). Ta có : \(n^2=3m^2+2\equiv2\left(mod3\right)\) ( loại )
TH 2 : \(\hept{\begin{cases}2x-1=m^2\\2x+1=3n^2\end{cases}}\) . Dễ thấy m lẻ \(\Rightarrow m=2k+1\)
Khi đo s: \(2x-1=\left(2k+1\right)^2\)
\(\Rightarrow x^2=k^2+\left(k+1\right)^2\) ( đpcm )
Tại sao 2x+1 và 2x-1 lại nguyên tố cùng nhau vậy bạn?
Chứng minh nó nguyên tố :
Đặt \(\left(2x-1,2x+1\right)=d\)
Khi đó : \(\hept{\begin{cases}2x-1⋮d\\2x+1⋮d\end{cases}}\) \(\Rightarrow2⋮d\Rightarrow d\in\left\{1,2\right\}\)
Mà : \(2x-1⋮̸2\)
Vì vậy : \(d=1\)
Cho x2 +2y là số chính phương với x,y là số tự nhiên .Chứng minh x2 +y bằng tổng 2 số chính phương
tìm 2 số tự nhiên biết bình phương của tổng 2 số đó lớn hơn bình phương của hiệu 2 số đó bằng 48
Xét tính đúng sai của các mệnh đề sau:
(1) Với mọi số tự nhiên \(x,\,\,\sqrt x \) là số vô tỉ;
(2) Bình phương của mọi số thực đều không âm;
(3) Có số nguyên cộng với chính nó bằng 0;
(4) Có số tự nhiên n sao cho 2n – 1 = 0.
(1) “Với mọi số tự nhiên \(x,\,\,\sqrt x \) là số vô tỉ” sai, chẳng hạn \(x = 1:\;\sqrt x = 1\) không là số vô tỉ.
(2) “Bình phương của mọi số thực đều không âm” đúng;
(3) “Có số nguyên cộng với chính nó bằng 0” đúng, số nguyên đó chính là số 0;
(4) “Có số tự nhiên n sao cho 2n – 1 = 0” sai, vì chỉ khi \(n = \frac{1}{2}\) thì 2n – 1 = 0 nhưng \(\frac{1}{2}\) không phải là số tự nhiên.
Đúng 0
Bình luận (0)
1) Tìm 5 số nguyên sao cho mỗi số trong đó đều bằng bình phương của tổng 4 số còn lại.
2) Tìm x, y là số tự nhiên khác 0 để đồng thời x+1 chia hết cho y và y+1 chia hết cho x
căn bậc hai của x bình trừ 3x cộng 17 là 1số tự nhiên khi x bằng mấy ?














