Cho hình bình hành ABCD. Vẽ AH vuông góc với CD, AK vuông góc với BC. CMR: Tam giác KAH đồng dạng với tam giác ABC
Những câu hỏi liên quan
cho hình bình hành ABCD . Vẽ AH vuông góc vs CD ; AK vuông góc với BC
CMR: tam giác KAH đồng dao với tam giác ABC
Bài 1:Cho hình thang ABCD có AB//CD , góc A=D=90 độ, AB=2cm,CD=4.5,BC=3. Chứng minh BC và BD vuông góc.
Bài 2: Cho hình bình hành ABCD. Vẽ AH vuông góc CD tại H,AK vuông góc BC tại K. Chứng minh tam giác KAH đồng dạng ABC
Mình đang cần gấp, giúp mình với !
cho hình bình hành abcd, góc A tù, AK vuông góc với BC,AH vuông góc với CD.cm tam giác ABC đồng dạng với tam giác AHK
cho hình bình hành ABCD. Từ A kẻ AM vuông góc với BC, AN vuông góc với CD ( M thuộc BC, N thuộc CD).
CMR: tam giác MAN đồng dạng với tam giác ABC
cho hình bình hành ABCD. Từ A kẻ AM vuông góc với BC, AN vuông góc với CD ( M thuộc BC, N thuộc CD).
CMR: tam giác MAN đồng dạng với tam giác ABC
Cho hình bình hành ABCD có góc B nhọn. Từ A kẻ AM vuông góc với BC (M thuộc BC), kẻ AN vuông góc với CD (N thuộc CD). CMR:
a. Tam giác AND đồng dạng với tam giác AMB.
b. Tam giác MAN đồng dạng với tam giác ABC
Hình bình hành ABCD có AM vuông góc với BC, AN vuông góc với DC. CMR:
a) Tam giác ADN đồng dạng với tam giác ABN
b) Tam giác MAN đồng dạng với tam giác ABC
c) Giả sử AC là đường chéo lớn của hbh ABCD, vẽ CE vuông góc với AB, CF vuông góc với AD. CMR: AB.AE+AD.AF=AC^2.
Cho hình bình hành ABCD .Từ A kẻ AM vuông góc với BC,AN vuông góc CD (M thuộc BC và N thuộc CD). Chứng mình rằng tam giác MAN đồng dạng với tam giác ABC.
* Trường hợp góc B nhọn:
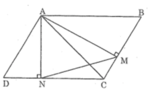
Xét △ AMB và △ AND, ta có:
∠ (AMB) = ∠ (AND) = 90 0
B = D (t/chất hình bình hành) ⇒ △ AMB đồng dạng △ AND (g.g)
Suy ra: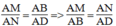 
Mà AD = BC (t/chất hình hình hành)
Suy ra: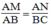 
Lại có: AB // CD (gt)
AN ⊥ CD (gt)
Suy ra: AN ⊥ AB hay ∠ (NAB) = 90 0
suy ra: ∠ NAM + ∠ MAB = 90 0 (1)
Trong tam giác vuông AMB ta có ∠ ABM = 90 0
Suy ra: ∠ (MAB) + ∠ B = 90 0 (2)
Từ (1) và (2) suy ra: ∠ NAM = ∠ B
Xét △ ABC và △ MAN ta có:
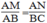(chứng minh trên)
∠ (NAM) = ∠ B (chứng minh trên)
Vậy △ ABC đồng dạng △ MAN (c.g.c)
* Trường hợp góc B tù:
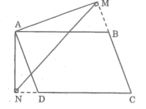
Xét △ MAN và △ AND, ta có:
∠ (AMB) = ∠ (AND) = 90 0
∠ (ABM) = ∠ (ADN) (vì cùng bằng C)
⇒ △ AMB đông dạng △ AND (g.g)
Suy ra: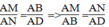
Mà AD = BC (t/chẩt hình bình hành)
Suy ra: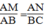 
Vì AB //CD nên ∠ (ABC) + ∠ C = 180 0 (3)
Tứ giác AMCN có ∠ (AMC) = ∠ (AND) = 90 0
Suy ra: ∠ (MAN) + ∠ C = 180 0 (4)
Từ (3) và (4) suy ra: (MAN) = (ABC)
Xét △ AMN và △ ABC, ta có:
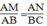(chứng minh trên)
∠ (MAN) = ∠ (ABC) (chứng minh trên)
Vậy △ MAN đồng dạng △ ABC (c.g.c)
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD. Từ A kẻ AM vuông góc với BC, AN vuông góc với CD (M thuộc BC và N thuộc CD).
Chứng minh rằng tam giác MAN đồng dạng với tam giác ABC ?
