Với \(c=0\Rightarrow f\left(x\right)=0\) có nghiệm \(x=0\) (loại)

TH1: \(a;c\) trái dấu 

Xét pt \(f\left(x\right)=0\Leftrightarrow a\left(ax^2+bx+c\right)^2+b\left(ax^2+bx+c\right)+c=0\)

Đặt \(ax^2+bx+c=t\) \(\Rightarrow at^2+bt+c=0\) (1)

Do a; c trái dấu \(\Leftrightarrow\) (1) luôn có 2 nghiệm trái dấu.

Không mất tính tổng quát, giả sử \(t_1< 0< t_2\)

\(\Rightarrow\left[{}\begin{matrix}ax^2+bx+c=t_1\\ax^2+bx+c=t_2\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}ax^2+bx+c-t_1=0\left(2\right)\\ax^2+bx+c-t_2=0\left(3\right)\end{matrix}\right.\)

Mà a; c trái dấu nên:

- Nếu \(a>0\Rightarrow c< 0\Rightarrow c-t_2< 0\Rightarrow a\left(c-t_2\right)< 0\)

\(\Rightarrow\) (3) có nghiệm hay \(f\left(x\right)=0\) có nghiệm (loại)

- Nếu \(a< 0\Rightarrow c>0\Rightarrow c-t_1>0\Rightarrow a\left(c-t_1\right)< 0\)

\(\Rightarrow\left(2\right)\) có nghiệm hay \(f\left(x\right)=0\) có nghiệm (loại)

Vậy đa thức \(f\left(x\right)\) luôn có nghiệm khi a; c trái dấu

\(\Rightarrow\)Để \(f\left(x\right)=0\) vô nghiệm thì điều kiện cần là \(a;c\) cùng dấu \(\Leftrightarrow ac>0\)

Khi đó xét \(g\left(x\right)=0\) có \(a.\left(-c\right)< 0\Rightarrow g\left(x\right)=0\) luôn có 2 nghiệm trái dấu (đpcm)

f(0) = 1

\(\Rightarrow\) a.0² + b.0 + c = 1 

\(\Rightarrow\) c = 1

Vậy hệ số a = 0; b = 0; c = 1

f(1) = 2

\(\Rightarrow\) a.1² + b.1 + c = 2

\(\Rightarrow\) a + b + c = 2

Vậy hệ số a = 1; b = 1; c = 1

f(2) = 4

\(\Rightarrow\) a.2² + b.2 + c = 4

\(\Rightarrow\) 4a + 2b + c = 4

Vậy hệ số a = 4; b = 2; c = 1

Chúc bn học tốt! (chắc vậy :D)

Hàm số f(x) đâu có y,z (y là tên hàm số rồi còn gì)??

ĐK: \(x\inℤ\)

TA có: \(y=f\left(x\right)=ax^2+bx+c⋮5\)

Vậy \(f\left(x\right)=ax^2+bx+c\) có dạng \(5k\) (k nguyên)

Nếu \(x⋮5\Rightarrow x\)có dạng \(5t\)

Thay vào,ta có: \(f\left(x\right)=25at^2+5bt+c=5t\left(5at+b\right)+c=5k\)  (1)

Suy ra \(c=5k-5t\left(5at+b\right)=5\left[k-t\left(5at+b\right)\right]\)  (2)

Thay (2) và (1) suy ra nếu x chia hết cho 5 thì f(x) chia hết cho 5 (thỏa mãn)

Nếu \(x⋮̸5\Rightarrow x\) có dạng 5t + 1

Thay vào và chứng minh tương tự để suy ra nếu x không chia hết cho 5 thì f(x) không chia hết cho 5 (trái với giả thiết)

Từ đó suy ra đpcm

Lời giải:Đặt $A=f(1)=a+b+c; B=f(-1)=a-b+c; C=f(0)=c$

Theo đề bài: $|A|, |B|, |C|\leq 1$

\(|a|+|b|+|c|=|\frac{A+B}{2}-C|+|\frac{A-B}{2}|+|C|\)

\(\leq |\frac{A+B}{2}|+|-C|+|\frac{A-B}{2}|+|C|=|\frac{A}{2}|+|\frac{B}{2}|+|C|+|\frac{A}{2}|+|\frac{-B}{2}|+|C|\)

\(=|A|+|B|+2|C|\leq 1+1+2=4\) (đpcm)

Mình có nghĩ ra cách này mọi người xem giúp mình với

f(x) = \(ax^2+bx+c\) 

Ta có f(0) = 2 => c = 2

Ta đặt Q(x) = \(ax^2+bx+c-2020\)

và G(x) = \(ax^2+bx+c+2021\)

f(x) - 2020 chia cho x - 1 hay Q(x) chia cho x - 1 được số dư

\(R_1\) = Q(1) = \(a.1^2+b.1+c-2020=a+b+c-2020\)  

Mà Q(x) chia hết cho x-1 nên \(R_1\) = 0

hay \(a+b+c-2020=0\). Mà c = 2 => a + b = 2018 (1)

G(x) chia cho x + 1 số dư 

\(R_2\) = G(-1) = \(a.\left(-1\right)^2+b.\left(-1\right)+c+2021=a-b+2+2021\)

Mà G(x) chia hết cho x + 1 nên \(R_2\)=0

hay \(a-b+2+2021=0\) => \(a-b=-2023\) (2)

Từ (1) và (2) suy ra: \(\left\{{}\begin{matrix}a+b=2018\\a-b=-2023\end{matrix}\right.\)

Vậy \(\left\{{}\begin{matrix}a=-\dfrac{5}{2}\\b=\dfrac{4041}{2}\end{matrix}\right.\)

ko biết !!!

\(f\left(0\right)=2\Rightarrow c=2\)

\(f\left(x\right)-2020\) chia hết \(x-1\Rightarrow f\left(1\right)-2020=0\)

\(\Rightarrow a+b+c-2020=0\Rightarrow a+b-2018=0\)

\(f\left(x\right)+2021\) chia hết \(x+1\Rightarrow f\left(-1\right)+2021=0\)

\(\Rightarrow a-b+c+2021=0\Rightarrow a-b+2023=0\)

\(\Rightarrow\left\{{}\begin{matrix}a+b=2018\\a-b=-2023\end{matrix}\right.\)  \(\Rightarrow\left\{{}\begin{matrix}a=\dfrac{5}{2}\\b=\dfrac{4041}{2}\end{matrix}\right.\)

Từ điều kiện đề bài \(\Rightarrow\left\{{}\begin{matrix}a+b+c=8\\-\dfrac{b}{2a}=2\\\dfrac{4ac-b^2}{4a}=9\end{matrix}\right.\Rightarrow f\left(x\right)=-x^2+4x+5\)

a. Không tồn tại m để \(3\left|f\left(x\right)\right|+m-5=0\) có 3 nghiệm phân biệt (nếu pt đã cho có 3 nghiệm thì 1 nghiệm trong đó luôn là nghiệm kép). Có 3 nghiệm thì được (khi đó \(\dfrac{5-m}{3}=9\Rightarrow m\))

b. \(2f\left(\left|x\right|\right)-7+5m=0\Leftrightarrow f\left(\left|x\right|\right)=\dfrac{-5m+7}{2}\) (1)

Đồ thì hàm \(y=f\left(\left|x\right|\right)\) (tạo ra bằng cách bỏ phần bên trái trục Oy và lấy đối xứng phần bên phải của đồ thị \(y=f\left(x\right)\) qua):

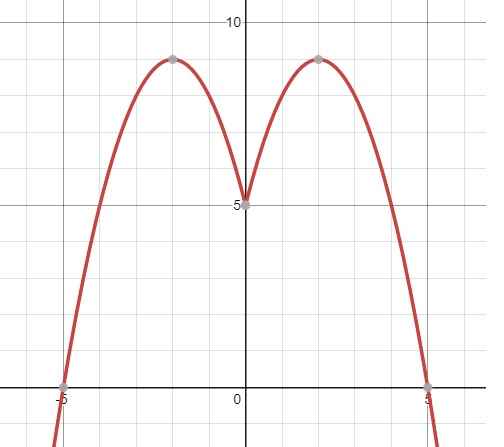
Từ đồ thị ta thấy (1) có 4 nghiệm pb khi:

\(5< \dfrac{-5m+7}{2}< 9\) \(\Rightarrow-\dfrac{11}{5}< m< -\dfrac{3}{5}\)

Đề đúng chưa v