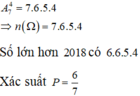Xét các số gồm 7 chữ số phân biệt được lập từ các số từ 1 đến 71/ Hỏi có 3 số a;b;c mà a+b=c không?2/ Hỏi có hai số khác nhau a, b mà a chia hết cho b không?
Xét các số gồm 7 chữ số phân biệt được lập từ các số từ 1 đến 71/ Hỏi có 3 số a;b;c mà a+b=c không?2/ Hỏi có hai số khác nhau a, b mà a chia hết cho b không?
Từ các chữ số từ 1 đến 9 có thể lập được bao nhiêu số tự nhiên có 3 chữ sô phân biệt chia hết cho 3
Các chữ số từ 1 đến 9 có tổng cộng 9 chữ số. Để số có ba chữ số chia hết cho 3, tổng của các chữ số đó cũng phải chia hết cho 3.
Có hai trường hợp để tìm số thỏa mãn:
Trường hợp tổng ba số là 9: Có thể lập ra các số sau: 369, 639, 693, 963.
Trường hợp tổng ba số là 18: Có thể lập ra các số sau: 189, 279, 369, 459, 549, 639, 729, 819, 918.
Vậy có tổng cộng 9 số tự nhiên có 3 chữ số phân biệt và chia hết cho 3.
Chia các chữ số từ 1 đến 9 làm 3 tập \(A=\left\{3;6;9\right\}\) ; \(B=\left\{1;4;7\right\}\) ; \(C=\left\{2;5;8\right\}\)
Số có 3 chữ số chia hết cho 3 khi:
TH1: 3 chữ số của nó thuộc cùng 1 tập \(\Rightarrow3.3!=18\) số
TH2: 3 chữ số của nó thuộc 3 tập phân biệt:
Chọn ra mỗi tập một chữ số có \(3.3.3=27\) cách
Hoán vị 3 chữ số có: \(3!=6\) cách
\(\Rightarrow27.6=162\) số
Như vậy có tổng cộng \(18+162=180\) số thỏa mãn
Gọi M là tập hợp tất cả các số gồm 2 chữ số phân biệt được lập từ các chữ số 1,2,3,4,5,6. Lấy ngẫu nhiên một số từ M, tính xác suất để số đó có tổng hai chữ số lớn hơn 7
A. 3 5
B. 2 7
C. 3 4
D. 2 5
Gọi M là tập hợp tất cả các số gồm 2 chữ số phân biệt được lập từ các chữ số 1,2,3,4,5,6. Lấy ngẫu nhiên một số từ M, tính xác suất để số đó có tổng hai chữ số lớn hơn 7.
A. 
B. 
C. 
D. 
Đáp án D
Có 6 cặp số có tổng lớn hơn 7 là (5;3); (5;4); (6;2); (6;3); (6;4); (6;5) nên ứng với 12 số có hai chữ số khác nhau mà có tổng lớn hơn 7.
Mặt khác, số các số có hai chữ số khác nhau được lập từ các chữ số 1; 2; 3; 4; 5; 6 là 
= 30 số.
Do đó, xác suất là:
Chọn ngẫu nhiên một số tự nhiên gồm bốn chữ số phân biệt được lập thành từ các chữ số 1, 2, 3, 4, 5, 6, 7. Tính xác suất để số được chọn lớn hơn 2018.
A. 4 7 .
B. 6 7 .
C. 5 7 .
D. 1 7 .
Bạn Sáu viết 7 số khác nhau , mỗi số gồm 7 chữ số phân biệt từ các chữ số 1,2,3,4,5,6,7 . Hỏi bạn Sáu có thể viết được đẳng thức sao cho tổng các lũy thừa bậc 7 của một vài số ( phân biệt ) trong 7 số này bằng tổng các lũy thừa bậc 7 của tất cả các số ( phân biệt ) còn lại ?
A = {1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 ; 9}
Hỏi từ A lập được bao nhiêu số có 5 chữ số phân biệt và có đúng 2 chữ số lẻ ?
Lời giải:
Gọi số thỏa mãn đề là $M$
Có $C^2_5$ cách chọn ra 2 số lẻ từ tập A
Với mọi cách chọn, có $A^2_5$ cách xếp 2 số lẻ đó trong $M$
Ba chữ số còn lại từ $(2;4;6;8)$ có $A^3_4$ cách chọn
Vậy số chữ số thỏa mãn: $C^2_5.A^2_5.A^3_4=4800$ số
1. Gọi S là tập hợp tất cả các số tự nhiên gồm 4 chữ số khác nhau được chọn từ các chữ số từ 1 đến 7 chọn ngẫu nhiên 1 số từ S tính xác suất để số được chọn là số lẻ và có mặt chữ số 5.
2. Tập hợp E gồm các chữ số từ 1 đến 5. Gọi M là tập hợp tatts cả các số tự nhiên có ít nhất 3 chữ số đôi 1 khác nhau. Lấy 1 số từ M tính xác suất để tổng các chữ số của số đó bằng 10.
3. Từ các chữ số 0,1,2,3,4,5,6,7 có thể lập được bao nhiêu số tự nhiên gồm 5 chữ số khác nhautrong đó có đúng 2 chữ số chẵn
