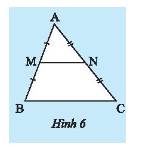
Cho \(M,N\) lần lượt là trung điểm của hai cạnh \(AB;AC\) của tam giác \(ABC\).
a) Tính các tỉ số \(\frac{{AM}}{{AB}},\frac{{AN}}{{AC}}\);
b) Chứng mình \(MN//BC\);
c) Chứng minh \(\frac{{MN}}{{BC}} = \frac{1}{2}\).
Những câu hỏi liên quan
Cho tam giác ABC; M và N lần lượt là trung điểm của hai cạnh AB và AC. Lấy điểm P sao cho N là trung điểm của đoạn thẳng MP.chứng minh rằng a, CP// AB, CP =AB/2
a: Xét ΔNAM và ΔNCP có
NA=NC
\(\widehat{ANM}=\widehat{CNP}\)
NM=NP
Do đó: ΔNAM=ΔNCP
=>\(\widehat{NAM}=\widehat{NCP}\)
mà hai góc này là hai góc ở vị trí so le trong
nên CP//AM
=>CP//AM
ΔNAM=ΔNCP
=>AM=CP
mà \(AM=\dfrac{AB}{2}\)
nên \(CP=\dfrac{AB}{2}\)
Đúng 1
Bình luận (1)
Cho tam giác ABC, M và N lần lượt là trung điểm của các cạnh bên AB và AC. Nối M với N, diện tích tam giác AMN là 18 cm2 . Tính diện tích tam giác ABC.
Bài 6. Cho tam giác ABC, M và N lần lượt là trung điểm của các cạnh bên AB và AC. Nối M với N, diện tích tam giác AMN là 9 cm2 . Tính diện tích tam giác ABC
giúp mk với
Cho hình thang cân ABCD. Gọi P là giao điểm của hai cạnh bên; M và N lần lượt là trung điểm của AB và CD. Chứng minh:P; M; N; O thẳng hàng
GIÚP MÌNH NHÉ! PLS
Cho tam giác ABC. Trên hai cạnh AB, AC lấy hai điểm E, F sao cho EF ∥ BC. Gọi H, G lần lượt là hình chiếu vuông góc của E, F lên BC. Gọi M, N lần lượt là trung điểm của BC và đường cao AI. Chứng minh rằng BN đi qua trung điểm của EH và MN đi qua trung điểm của HF.
Gọi P là giao của BN với EH; Q là giao của MN với HF; K là giao của MN với EF
Ta có
\(EH\perp BC;AI\perp BC\)=> EH//AI \(\Rightarrow\frac{PE}{NA}=\frac{PH}{NI}\) (Talet) \(\Rightarrow\frac{PE}{PH}=\frac{NA}{NI}=1\Rightarrow PE=PH\)
=> BN đi qua trung điểm P của EH
Ta có
EF//BC (gt) => KF//HM \(\Rightarrow\frac{QK}{QM}=\frac{QF}{QH}=\frac{KF}{HM}\) (Talet) => KH//FM
Xét tứ giác KFMH có
KF//HM; KH//FM => KFMH là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
=> KF=HM (Trong hình bình hành các cạnh đối bằng nhau)
\(\Rightarrow\frac{QF}{QH}=\frac{KF}{HM}=1\Rightarrow QF=QH\)
=> MN đi qua trung điểm Q của HF
Cho tam giác ABC, trên cạnh AB và AC lần lượt lấy hai điểm D và E sao cho BD = CE. Gọi M và N lần lượt là trung điểm của BC và DE. Đường thẳng qua M và N lần lượt cắt AB và AC tại P và Q. Chứng minh rằng góc MPB bằng góc MQC.
cho tam giác ABC có BC=8cm.Gọi D và E lần lượt là trung điểm của cạnh AB và AC,M và N lần lượt là trung điểm của các cạnh BC và CE.Tính MN.
Cho tam giác ABC. Gọi M, N lần lượt là trung điểm của các cạnh AC, AB. Trên các đường thẳng BM và CN lần lượt lấy các điểm D và E sao cho M là trung điểm của BD và N là trung điểm của EC. Chứng minh ba điểm E, A, D thẳng hàng.
Câu 1:Cho tam giác ABC. Gọi P,Q lần lượt là trung điểm của AB,AC. Trên tia đối của tia PC lấy ddierm D sao cho PCPD, trên tia đối của tia QB Lấy điểm E sao cho QE,QB. Chwusng min h ba điểm D,AE thẳng hàng.Câu 2 :Cho góc xOy. TRên cạnh Ox lấy hai điểm A và C. Trên cạnh Oy láy hai điểm B và D sao cho OAOB, OCOD.Gọi M,N lần lượt là trung điểm của AB và CD.a)Chứng minh đường thẳng OM là trung trực của AB.b)Chứng minh ba điểm O,M,N thẳng hàng.
Đọc tiếp
Câu 1:Cho tam giác ABC. Gọi P,Q lần lượt là trung điểm của AB,AC. Trên tia đối của tia PC lấy ddierm D sao cho PC=PD, trên tia đối của tia QB Lấy điểm E sao cho QE,QB. Chwusng min h ba điểm D,AE thẳng hàng.
Câu 2 :Cho góc xOy. TRên cạnh Ox lấy hai điểm A và C. Trên cạnh Oy láy hai điểm B và D sao cho OA=OB, OC=OD.Gọi M,N lần lượt là trung điểm của AB và CD.
a)Chứng minh đường thẳng OM là trung trực của AB.
b)Chứng minh ba điểm O,M,N thẳng hàng.
bạn sửa đề đi mk vừa nhìn đã bt có 1 chỗ sai ở câu 1
Đúng 0
Bình luận (0)
Bài 5: Cho tam giác ABC vuông tại A. Gọi M, N lần lượt là trung điểm của hai cạnh AB và BC.a) Gọi D là điểm đối cứng của A qua N. Chứng minh tứ giác ABCD là hình chữ nhật.b) Lấy I là trung điểm của cạnh AC và E là điểm đối xứng của N qua I.Chứng minh tứ giác ANCE là hình thoi.c) Đường thẳng BC cắt DM và DI lần lượt tại G và G’. Chứng minh BG CG’.d) Cho AB 6cm, AC 8cm. Tính diện tích ΔDGG’.
Đọc tiếp
Bài 5: Cho tam giác ABC vuông tại A. Gọi M, N lần lượt là trung điểm của hai cạnh AB và BC.
a) Gọi D là điểm đối cứng của A qua N. Chứng minh tứ giác ABCD là hình chữ nhật.
b) Lấy I là trung điểm của cạnh AC và E là điểm đối xứng của N qua I.
Chứng minh tứ giác ANCE là hình thoi.
c) Đường thẳng BC cắt DM và DI lần lượt tại G và G’. Chứng minh BG = CG’.
d) Cho AB = 6cm, AC = 8cm. Tính diện tích ΔDGG’.
TK
a) Ta có: NB = NC (gt); ND = NA (gt)
⇒ Tứ giác ABDC là hình bình hành
có ∠A = 90o (gt) ⇒ ABDC là hình chữ nhật.
b) Ta có: AI = IC (gt); NI = IE (gt)
⇒ AECN là hình bình hành (hai đường chéo cắt nhau tại trung điểm mỗi đường).
mặt khác ΔABC vuông có AN là trung tuyến nên AN = NC = BC/2.
Vậy tứ giác AECN là hình thoi.
c) BN và DM là 2 đường trung tuyến của tam giác ABD; BN và MD giao nhau tại G nên G là trọng tâm tam giác ABD.
Tương tự G’ là trọng tâm của hai tam giác ACD
⇒ BG = BN/3 và CG’ = CN/3 mà BN = CN (gt) ⇒ BG = CG’
d) Ta có: SABC = (1/2).AB.AC = (1/2).6.6 = 24 (cm2)
Lại có: BG = GG’ = CG’ (tính chất trọng tâm)
⇒ SDGB = SDGG' = SDG'C = 1/3 SBCD
(chung đường cao kẻ từ D và đáy bằng nhau)
Mà SBCD = SCBA (vì ΔBCD = ΔCBA (c.c.c))
⇒SDGG' = 24/3 = 8(cm2)
Đúng 2
Bình luận (0)
Cho tam giác ABC có AB=AC .Trên hai cạnh AB và AC lần lượt lấy 2 điểm M và N sao cho AM=AN . Gọi D,E làm lượt là trung điểm của MN và BC .CMR : 3 điểm A,E,D thẳng hàng
mik chx hiểu câu hỏi bn là j lun á
Đúng 0
Bình luận (0)