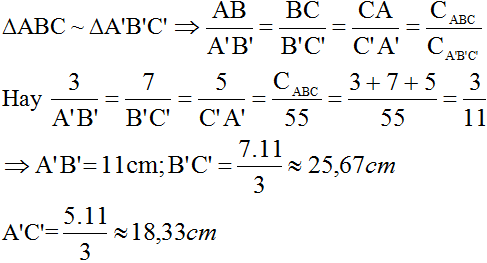cho a'b'c là các chữ số (a;b khác 0) thoả mãn a.bcd.abc=abcabc khi đó abcd bằng
Những câu hỏi liên quan
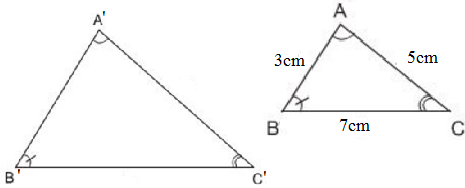
Tam giác ABC có độ dài các cạnh là AB = 3cm, AC = 5cm, BC = 7cm. Tam giác A'B'C' đồng dạng với tam giác A'B'C' và có chu vi bằng 55cm.
Hãy tính độ dài của các cạnh tam giác A'B'C' (làm tròn đến chữ số thập phân thứ hai).
Chu vi tam giác ABC là: AB + BC + CA = 3 + 7 + 5 = 15 (cm)
Δ A’B’C’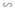 
ΔABC ⇒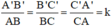 
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
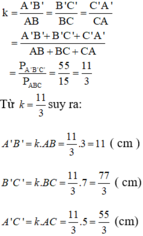
Đúng 1
Bình luận (0)
Cho Δ A'B'C' ∼ Δ A''B''C'' theo tỉ số đồng dạng k 1 , Δ A''B''C'' ∼ Δ ABC theo tỉ số đồng dạng là k 2 . Hỏi Δ A''B''C'' ∼ Δ A'B'C' và Δ A'B'C' ∼ Δ ABC đồng dạng theo tỉ số nào?
Cho Δ A'B'C' ∼ Δ A''B''C'' theo tỉ số đồng dạng k 1 , Δ A''B''C'' ∼ Δ ABC theo tỉ số đồng dạng là k 2 . Hỏi Δ A''B''C'' ∼ Δ A'B'C' và Δ A'B'C' ∼ Δ ABC đồng dạng theo tỉ số nào?
Tam giác ABC có độ dài các cạnh là AB = 3cm, AC = 5cm, BC = 7cm. Tam giác A'B'C' đồng dạng với tam giác ABC và có chu vi bằng 55 cm
Hãy tính độ dài các cạnh của tam giác A'B'C' (làm tròn đến chữ số thập phân thứ hai) ?
∆ABC ∽ ∆A'B'C' => = = =
hay = = = =
=> A'B' = 11cm;
B'C' = ≈ 25.67 cm
A'C' = ≈ 18,33 cm
Đúng 0
Bình luận (0)
a) Nếu \(\Delta A'B'C' = \Delta ABC\) thì tam giác \(A'B'C'\) có đồng dạng với tam giác \(ABC\) không? Tỉ số đồng dạng là bao nhiêu?
b) Cho tam giác \(\Delta A'B'C'\backsim\Delta ABC\) theo tỉ số đồng dạng \(k\) thì \(\Delta ABC\backsim\Delta A'B'C'\) theo tỉ số nào?
a) Nếu \(\Delta A'B'C' = \Delta ABC\) thì tam giác \(A'B'C'\) đồng dạng với tam giác \(ABC\). Vì hai tam giác bằng nhau có các góc tương ứng bằng nhau và các cạnh tương ứng bằng nhau.
Khi đó, \(\left\{ \begin{array}{l}\widehat A = \widehat {A'};\widehat B = \widehat {B'};\widehat C = \widehat {C'}\\\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = 1\end{array} \right.\). Vậy \(\Delta A'B'C'\backsim\Delta ABC\) và tỉ số đồng dạng là 1.
b) Vì \(\Delta A'B'C'\backsim\Delta ABC\) theo tỉ số đồng dạng là \(k\) nên tỉ số đồng dạng là: \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = k\).
Khi đó, \(\Delta ABC\backsim\Delta A'B'C'\) đồng dạng với tỉ số đồng dạng là: \(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{{BC}}{{B'C'}} = \frac{1}{k}\).
Vậy \(\Delta ABC\backsim\Delta A'B'C'\)theo tỉ số \(\frac{1}{k}\).
Đúng 1
Bình luận (0)
Cho tam giác ABC đồng dạng với tam giác ABC . Cho biết
A
B
16
,
2
c
m
,
B
C
24
,
3
c
m
,
C
A
32
,
4
c
m
, hãy tính độ dài các cạnh của tam giác ABC nếu:a) AB lớn hơn AB là 10cm;b) AB lớn hơn AB là 10c...
Đọc tiếp
Cho tam giác ABC đồng dạng với tam giác A'B'C' . Cho biết A B = 16 , 2 c m , B C = 24 , 3 c m , C A = 32 , 4 c m , hãy tính độ dài các cạnh của tam giác A'B'C' nếu:
a) AB lớn hơn A'B' là 10cm;
b) A'B' lớn hơn AB là 10cm
Ta có
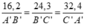
a) Tính được A'B' = 6,2cm. Từ đó tính được B'C' = 9,3cm và A'C' = 12,4cm.
b) Tương tự câu a tính được A'B' = 26,2cm, B'C' = 39,3cm và A'C' = 52,4cm
Đúng 0
Bình luận (0)
Cho tam giác abc có ab = 15,3 cm ; bc = 21,3 cm ; ac = 31,2 cm . tính độ dài cạnh của tam giác a'b'c' ( làm tròn đến chữ số thập phân thứ 2 , biết tam giác a'b'c' đồng dạng vs tam giác abc ) và :
a, A'B lớn hơn cạnh AB là 10,8 cm
b, A'B' bé hơn cạnh AB là 5,4
Giúp mình với :D
Các bn giúp mk với nha!!!!!!!!!!!!!!!!!!
Cho tam giác ∆ABC ~ ∆A'B'C' biết AB=8,1 cm; AC=16,35cm;BC=12,15cm.Tính độ dài các cạnh của tam giác A'B'C' biết:
a)A'B'>AB là 5,4 cm
b)A'B'<AB là 5,4 cm
Các bạn giúp mk với!mk k cho
Cho khối lăng trụ ABC. ABC. Gọi E là trọng tâm tam giác ABC và F là trung điểm BC. Tính tỉ số thể tích giữa khối B. EAF và khối lăng trụ ABC. ABC. A.
1
4
B.
1
8
C.
1
5
D.
1
6
Đọc tiếp
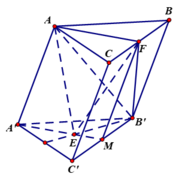
Cho khối lăng trụ ABC. A'B'C'. Gọi E là trọng tâm tam giác A'B'C' và F là trung điểm BC. Tính tỉ số thể tích giữa khối B'. EAF và khối lăng trụ ABC. A'B'C'.
A. 1 4
B. 1 8
C. 1 5
D. 1 6
