Biết tập nghiệm S của bất phương trình log3( 9x-2) < 1 là khoảng (a; b) . Tính hiệu số b- a
A. b- a= log910
B. b- a= 1
C. ![]()
D. 5![]()
Biết rằng tập nghiệm của bất phương trình log 3 ( x 2 - 3 x + 5 ) < 2 là khoảng a ; b . Giá trị của biểu thức a 2 + b 2 bằng
A. 15.
B. 7.
C. 11.
D. 17.
Đáp án D.
Ta có
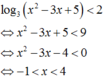
Suy ra a = - 1 , b = 4 Do đó a 2 + b 2 = 17 .
Phân tích phương án nhiễu.
Phương án A: Sai do HS giải đúng được a = - 1 , b = 4 nhưng lại tính sai a 2 + b 2 = 15 hoặc do HS giải sai bất phương trình. Cụ thể:
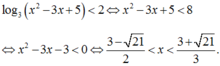
Suy ra a = 3 - 5 2 ; b = 3 + 5 2 Do đó tính được a 2 + b 2 = 15
Phương án B: Sai do HS giải sai bất phương trình. Cụ thể:
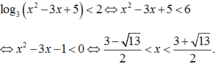
Suy ra a = 3 - 13 2 ; b = 3 + 13 2 Do đó tính được a 2 + b 2 = 11 .
Tập nghiệm của bất phương trình 2 log 3 ( x - 1 ) + log 3 ( 2 x - 1 ) ≤ 2 là
A. S = (1; 2]
B. S = ( - 1 2 ; 2 )
C. [1; 2]
D. [ - 1 2 ; 2 ]
Tập nghiệm của bất phương trình 2 log 3 ( x - 1 ) + log 3 ( 2 x - 1 ) ≤ 2 là
A. S = ( 1 ; 2 ]
B. S = ( - 1 / 2 ; 2 )
C. S = [ 1 ; 2 ]
D. S = [ - 1 / 2 ; 2 ]
Tập nghiệm của bất phương trình log3 (2x – 1) > 4 là:
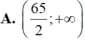
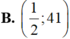
![]()
![]()
Đáp án C
Do cơ số lớn hơn 1 nên BPT tương đương
2x – 1 > 34 = 81 <=>2x > 82 <=> x > 41.
Tập nghiệm của bất phương trình log 3 ( x 2 + 2 ) ≤ 3 là
![]()
![]()
![]()
![]()
Biết tập nghiệm S của bất phương trình log π 6 log 3 x - 2 > 0 là khoảng (a;b). Tính b – a.
A. 2
B. 4
C. 3
D. 5
Biết tập nghiệm S của bất phương trình log π 6 log 3 x - 2 > 0 là khoảng (a;b). Tính b - a.
A. 2
B. 4
C. 3
D. 5
Đáp án A.
Ta có: log π 6 log 3 x - 2 > 0 ⇔ 0 < log 3 x - 2 < 1 ⇔ x - 2 > 1 x - 2 < 3 ⇔ 3 < x < 5
Vậy S = 3 ; 5 ⇒ b - a = 2 .
Tìm tập nghiệm của bất phương trình log3(2x-1) > log9x2
![]()
![]()
![]()
![]()
Tìm tập nghiệm của bất phương trình log 3 ( 2 x - 3 ) > 1
A. ( 1 ; + ∞ )
B. ( 1 6 ; + ∞ )
C. ( 2 ; + ∞ )
D. ( 3 ; + ∞ )