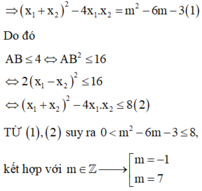Cho 4 số a, b, x, y sao cho ab=1; ax+by=1. CMR xy\(\le\)1

Những câu hỏi liên quan
Cho 4 số a, b, x, y sao cho ab=1; ax+by=1. CMR xy\(\le\)1
\(\left(ax+by\right)^2=1\Leftrightarrow\left(ax\right)^2+2abxy+\left(by\right)^2=1\Leftrightarrow2xy\le1\Leftrightarrow xy\le\frac{1}{2}\)
Đúng 0
Bình luận (0)
Có bao nhiêu số nguyên dương m sao cho đường thẳng yx+m cắt đồ thị hàm số
y
2
x
-
1
x
+
1
tại hai điểm phân biệt A, B và
A
B
≤
4
A. 1 B. 6 C. 2 D. 7
Đọc tiếp
Có bao nhiêu số nguyên dương m sao cho đường thẳng y=x+m cắt đồ thị hàm số y = 2 x - 1 x + 1 tại hai điểm phân biệt A, B và A B ≤ 4
A. 1
B. 6
C. 2
D. 7
Có bao nhiêu số nguyên dương m sao cho đường thẳng
y
x
+
m
x
cắt đồ thị hàm số
y
2
x
−
1
x
+
1
tại hai điểm phân biệt A, B và
A
B
≤
4
A. 7 B. 6 C. 1 D. 2
Đọc tiếp
Có bao nhiêu số nguyên dương m sao cho đường thẳng y = x + m x cắt đồ thị hàm số y = 2 x − 1 x + 1 tại hai điểm phân biệt A, B và A B ≤ 4
A. 7
B. 6
C. 1
D. 2
Cho các số a,b,x, y sao cho ab#0 và a khác -b thỏa mãn
\(\frac{x^4}{a}+\frac{y^4}{b}=\frac{1}{a+b}\) ; x2 +y2=1
Chứng minh : \(\frac{x^{2002}}{a^{1001}}+\frac{y^{2002}}{b^{1001}}=\frac{2}{\left(a+b\right)^{1001}}\)
\(\Leftrightarrow\frac{x^4}{a}+\frac{y^4}{b}=\frac{\left(x^2+y^2\right)^2}{a+b}\)
\(\Leftrightarrow\frac{x^4b+y^4a}{ab}=\frac{x^4+y^4+2x^2y^2}{a+b}\Leftrightarrow\left(a+b\right)\left(x^4b+y^4a\right)=ab\left(x^4+y^4+2x^2y^2\right)\)
\(\Leftrightarrow x^4ab+y^4a^2+x^4b^2+y^4ab=x^4ab+y^4ab+2x^2y^2ab\)
\(\Leftrightarrow y^4a^2+x^4b^2=2x^2y^2ab\Leftrightarrow\left(x^2b-y^2a\right)^2=0\Leftrightarrow\frac{x^2}{a}=\frac{y^2}{b}\)
\(\Rightarrow\left(\frac{x^2}{a}\right)^{1001}=\left(\frac{y^2}{b}\right)^{1001}\Leftrightarrow\frac{x^{2002}}{a^{1001}}=\frac{y^{2002}}{b^{2011}}\)
Mà: \(\frac{x^2}{a}=\frac{y^2}{b}=\frac{x^2+y^2}{a+b}=\frac{1}{a+b}\Leftrightarrow\left(\frac{x^2}{a}\right)^{1001}=\frac{1}{\left(a+b\right)^{1001}}\)
\(\Rightarrow\frac{x^{2002}}{a^{1001}}+\frac{y^{2002}}{b^{1001}}=\frac{2}{\left(a+b\right)^{1001}}\left(đpcm\right)\)
Đúng 0
Bình luận (0)
\(x^2+y^2=1\Rightarrow y^2=1-x^2\)
\(\frac{x^4}{a}+\frac{y^4}{b}=\frac{1}{a+b}\Leftrightarrow\frac{b.x^4+a.y^4}{ab}=\frac{1}{a+b}\)
\(\Leftrightarrow bx^4+ay^4=\frac{ab}{a+b}\Leftrightarrow bx^4+a\left(1-x^2\right)^2-\frac{ab}{a+b}=0\)
\(\Leftrightarrow bx^4+a\left(x^4-2x^2+1\right)-\frac{ab}{a+b}=0\)
\(\Leftrightarrow\left(a+b\right)x^4-2ax^2+a-\frac{ab}{a+b}=0\)
\(\Leftrightarrow\left(a+b\right)x^4-2ax^2+\frac{a^2}{a+b}=0\Leftrightarrow\left(a+b\right)\left[x^4-2.x.\frac{a}{a+b}+\left(\frac{a}{a+b}\right)^2\right]=0\)
\(\Leftrightarrow\left(a+b\right)\left(x^2-\frac{a}{a+b}\right)=0\Rightarrow x^2=\frac{a}{a+b}\) (do \(a+b\ne0\))
\(\Rightarrow y^2=1-x^2=\frac{b}{a+b}\)
\(\Rightarrow\) \(\frac{x^2}{a}=\frac{a}{a\left(a+b\right)}=\frac{1}{a+b}\) ; \(\frac{y^2}{b}=\frac{b}{b\left(a+b\right)}=\frac{1}{a+b}\)
Thay vào bài toán:
\(\frac{x^{2002}}{a^{1001}}+\frac{y^{2002}}{b^{1001}}=\left(\frac{x^2}{a}\right)^{1001}+\left(\frac{y^2}{b}\right)^{1001}=\left(\frac{1}{a+b}\right)^{1001}+\left(\frac{1}{a+b}\right)^{1001}=\frac{2}{\left(a+b\right)^{1001}}\)
Đúng 0
Bình luận (0)
x2+y2=1⇒y2=1−x2
x4a+y4b=1a+b⇔b.x4+a.y4ab=1a+b
⇔bx4+ay4=aba+b⇔bx4+a(1−x2)2−aba+b=0
⇔bx4+a(x4−2x2+1)−aba+b=0
⇔(a+b)x4−2ax2+a−aba+b=0
⇔(a+b)x4−2ax2+a2a+b=0⇔(a+b)[x4−2.x.aa+b+(aa+b)2]=0
⇔(a+b)(x2−aa+b)=0⇒x2=aa+b (do a+b≠0)
⇒y2=1−x2=ba+b
⇒ x2a=aa(a+b)=1a+b ; y2b=bb(a+b)=1a+b
Thay
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho hàm số
y
2
x
-
1
x
-
1
có đồ thị (C). Tìm tất cả các giá trị thực của tham số m để đường thẳng d: y x + m cắt (C) tại hai điểm phân biệt A, B sao cho AB 4 A. m -1 B.
[
m
0...
Đọc tiếp
Cho hàm số y = 2 x - 1 x - 1 có đồ thị (C). Tìm tất cả các giá trị thực của tham số m để đường thẳng d: y = x + m cắt (C) tại hai điểm phân biệt A, B sao cho AB = 4
A. m = -1
B. [ m = 0 m = 3
C. [ m = - 1 m = 3
D. m = 4
Đáp án C
Xét pt tương giao:
2 x - 1 x - 1 = x + m ⇔ 2 x - 1 - x + m x - 1 = 0 ⇔ x 2 - 3 - m x + m - 1 = 0
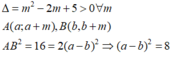
a + b 2 - 4 a b = 8 ⇔ 3 - m 2 - 4 1 - m = 8 ⇔ [ m = - 1 m = 3
Đúng 0
Bình luận (0)
Cho hàm số y
2
x
-
1
x
-
1
có đồ thị ( c ).Tìm tất cảc các giá trị thực của tham số m để đường thẳng: d: y x +m và cắt ( c ) tại hai điểm phân biệt A, B sao cho AB 4. A. m -1 B. C. D. m4
Đọc tiếp
Cho hàm số y = 2 x - 1 x - 1 có đồ thị ( c ).Tìm tất cảc các giá trị thực của tham số m để đường thẳng: d: y= x +m và cắt ( c ) tại hai điểm phân biệt A, B sao cho AB = 4.
A. m= -1
B. 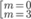
C. 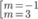
D. m=4
Cho a^2 + b^2 = c^2 + d^2 = 2017 và ac + bd = 0. Tính giá trị biểu thức S = ab + cd.
+ Cho a, b là các số nguyên dương sao cho: a + 1 và b + 2007 chia hết cho 6. Chứng minh: 4^a + a + b chia hết cho 6.
+ Cho x, y là các số thực dương thỏa mãn: x + y = (x – y)√xy. Tìm giá trị nhỏ nhất của P = x + y.
...............HELP ME , PLEASE...........
Cho a^2 + b^2 = c^2 + d^2 = 2017 và ac + bd = 0. Tính giá trị biểu thức S = ab + cd.
+ Cho a, b là các số nguyên dương sao cho: a + 1 và b + 2007 chia hết cho 6. Chứng minh: 4^a + a + b chia hết cho 6.
+ Cho x, y là các số thực dương thỏa mãn: x + y = (x – y)√xy. Tìm giá trị nhỏ nhất của P = x + y.
help me
1/cho số nguyên âm x và y thỏa mãn /x/=5 và /y/=11
2/viết tập hợp sau dưới dạng liệt kê C={100:4<x<113:4}
3/số tự nhiên n sao cho n^2 +404 là số chính phương
4/cho ab-ac+bc-c^2=-1 với a,b,c thuộc Z.khi đó a+b=?