Cho tam giác ABC có 3 góc nhọn. Vẽ đoạn thẳng AD vuông góc với AB và bằng AB(D khác phía C đối với AB),vẽ đoạn thẳng AE vuông góc với AC và bằng AC(E khác phía B đối với AC).CM; a, DC=BE;b, DC vuông góc BE
Giúp mình với, mình cần gấp!
Cho tam giác ABC có 3 góc nhọn. Vẽ đoạn thẳng AD vuông góc với AB và bằng AB(D khác phía C đối với AB),vẽ đoạn thẳng AE vuông góc với AC và bằng AC(E khác phía B đối với AC).CM; a, DC=BE;b, DC vuông góc BE
Cho tam giác ABC có ba góc nhọn. Vẽ đoạn thẳng AD vuông góc với AB và bằng AB (D khác phía C đối với AB), vẽ đoạn thẳng AE vuông góc với AC và bằng AC (E khác phía B đối với AC).Chứng minh rằng: DC = BE
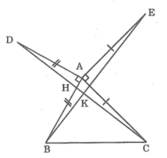
∠DAC = ∠DAB + ∠BAC = 90o + ∠BAC
∠BAE = ∠BAC + ∠CAE = ∠BAC + 90o
⇒ ∠DAC = ∠BAE
Xét ΔABE và ΔADC, ta có:

Cho tam giác ABC có ba góc nhọn. Vẽ đoạn thẳng AD vuông góc với AB và bằng AB (D khác phía C đối với AB), vẽ đoạn thẳng AE vuông góc với AC và bằng AC (E khác phía B đối với AC).Chứng minh rằng: DC ⊥BE
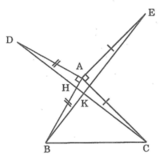
Gọi giao điểm DC và AB là H, giao điểm của CD và BE là K
Ta có: ΔABE = ΔADC (cmt)
⇒ ∠ABE = ∠ADC (hai góc t.ư)
hay ∠HBK = ∠ADH
+ ΔADH và ΔBKH đều có tổng ba góc trong mỗi tam giác bằng 180o nên có:
∠ADH + ∠DAH + ∠AHD = ∠BKH + ∠KHB + ∠HBK
Mà ∠AHD = ∠BHK (hai góc đối đỉnh)
∠ADH = ∠HBK (chứng minh trên)
Suy ra ∠DAH = ∠HKB
Mà ∠DAH = 90o nên ∠HKB = 90o
⇒ DC ⊥ BE (điều phải chứng minh)
Cho tam giác ABC có ba góc nhọn. Vẽ đoạn thẳng AD vuông góc với AB và bằng AB (D khác phía C đối với AB), Vẽ đoạn thẳng AE vuông góc với AC và bằng AC (E khác phía C đối với A) Chứng minh rằng :
DC=BE và DC vuông góc với BE
Ta có : \(\widehat{DAB}=\widehat{CAE}=90^0\Rightarrow\widehat{DAB}+\widehat{BAC}=\widehat{CAE}+\widehat{BAC}\)
hay \(\widehat{DAC}=\widehat{EAB}\)
Xét \(\Delta ADC\)và \(\Delta ABE\)có :
AD = AB
\(\widehat{DAC}=\widehat{EAB}\)
AC = AE
\(\Rightarrow\Delta ADC=\Delta ABE\left(c.g.c\right)\Rightarrow DC=BE\)
Vì tam giác ADC = tam giác ABE nên \(\widehat{AEB}=\widehat{ACD}\)
mà \(\widehat{AKE}=\widehat{BKC}\left(doi-dinh\right),\widehat{AKE}+\widehat{AEB}=90^0\)
\(\Rightarrow\widehat{BKC}+\widehat{AEB}=90^0\) hay góc \(\widehat{BKC}+\widehat{ACD}=90^0\)
\(\Rightarrow DC\perp BE\)
hỏi thật thì k ở đâu vậy ?
Cho tam giác ABC nhọn. Vẽ đoạn thẳng AD vuông góc với AB và bằng AB(D khác phía C đối với AB). Vẽ đoạn thẳng AE vuông góc với AC và bằng AC(E khác phía B đối với AC) Chứng minh rằng:
a/DC=BE
b/ DC vuông góc với BE
BÀI 1: Cho tam giác ABC có ba góc nhọn - Vẽ đoạn thẳng AD vuông gốc với AB và bằng AB ( D khác phía C đối với AB) vẽ đoạn thẳng AE vuông góc với AC và bằng AC (E khác phía B đối với AC) Chứng minh rằng :
1) DC = BE
2) DC I BE
Ta có: \(\widehat{DAC}=\widehat{DAB}+\widehat{BAC;}\widehat{BAE}=\widehat{EAC}+\widehat{BAC}.\)
Mà \(\widehat{DAB}=\widehat{EAC}\left(90^o\right);\widehat{BAC}chung.\)
\(\Rightarrow\) \(\widehat{DAC}=\widehat{BAE}.\)
Xét tam giác DAC và tam giác BAE:
+ AD = AB (gt).
+ AC = AE (gt).
+ \(\widehat{DAC}=\widehat{BAE}\left(cmt\right).\)
\(\Rightarrow\) Tam giác DAC = Tam giác BAE (c - g - c).
\(\Rightarrow\) DC = BE (2 cạnh tương ứng).
Cho tam giác ABC có 3 góc nhọn . Vẽ đoạn thẳng AD vuông góc với AB và bằng AB ( D khác phía C đối với AB) , vẽ đoạn thẳng AE vuông góc với AC và bằng AC ( E khác phía B đối với AC) . Chứng minh rằng :
a) DC=BE
b)DC vuông góc với BE
Cho tam giác ABC nhọn vẽ đoạn thẳng AD vuông góc với AB và AD=AB ( D khác phía C đối với AB ) vẽ đoạn thẳng AE vuông góc với AC và AE=AC( E khác phía B đối với AC) Cm:
a) DC=BE
b)DCvuông góc với BE
a) Xét 2 tam giác DAC và BAE, có:
DA = BA (gt) (1)
AC = AE (gt) (2)
Lại có: ^DAB = ^CAE = \(90^0\) (do AD vuông góc với AB, AE vuông góc với AC)
=> ^DAB + ^BAC = ^CAE + ^BAC
hay ^DAC = ^BAE (3)
Từ (1), (2) và (3), ta suy ra: \(\Delta\)DAC = \(\Delta\)BAE (c.g.c)
=> DC = BE (2 cạnh tương ứng)
b) Gọi giao điểm của BE và DC là O, giao điểm của AB và DC là I
Ta có: ^DIA = ^BIO (đối đỉnh)
^ADC = ^ABE (2 góc tương ứng do tg DAC = tg BAE)
Mà ^DIA + ^ADC = \(90^0\) (tam giác DAI vuông tại A)
=> ^BIO + ^ABE = \(90^0\)
=> ^BOI = \(90^0\)
=> DC vuông góc với BE
2. Vẽ tam giác ABC có 3 góc nhọn. Vẽ đoạn thẳng AD vuông góc và bằng AB (D khác phía C đối với AB), vẽ đoạn thẳng AE vuông góc và bằng AC (E khác phía B đối với AC). CMR: a. DC=BE/ b. DC vuông góc BE