Pls help me:
Cho tam giác ABC nội tiếp (O;R) . Biết AB=\(R\sqrt{2}\), AC=\(R\sqrt{2}\). Tính các góc của tam giác ABC

Những câu hỏi liên quan
Bai1: Cho tam giác ABC nội tiếp đường tròn tâm O bán kính R. Các đỉnh B, C cố định còn A chạy trên đường tròn đó. Tìm tập hợp các trọng tâm G của tam giác ABC khi A di độngCho tam giác ABC nội tiếp đường tròn tâm O bán kính R. các bạn giúp mih` giải và vẽ hình bài này nhé help me đang cần gấp
Cho ba đường tròn (O1); (O2); (O3) cùng bán kính R tiếp xúc ngoài từng đôi một. Các tiếp tuyến chung ngoài cắt nhau từng đôi một tại A,B,C. Cho biết dạng của tam giác ABC và tính diện tích tam giác đó. Pls help.
cho tam giắc abc kể các đường cao AH và BK . CM tứ giác AKHB và tức giác CKIH nội tiếp( I là giao điểm của AH và DK)
GIÚP MÌNH VỚI PLS
Xét tứ giác AKHB có
\(\widehat{AKB}=\widehat{AHB}=90^0\)
Do đó: AKHB là tứ giác nội tiếp
Xét tứ giác CKIH có
\(\widehat{CKI}+\widehat{CHI}=180^0\)
Do đó: CKIH là tứ giác nội tiếp
Đúng 0
Bình luận (0)
Cho tam giác ABC nội tiếp (O) , I là tâm dt nội tiếp của ABC , AI cắt (O) tại J, JO cắt (O) tại K và cắt BC tại E .
1,CMR: JE.JK=JI^2
2,các tiếp tuyến tại B và C của (O) cắt nhau tại S.CMR: SJ.EK=SK.EJ
help.
cho tam giác abc nội tiếp đường tròn (o), I là tâm đường tròn nội tiếp tam giác abc. AI cắt (o) tại M, c/m tam giác MIB cân
Cho tam giác ABC đều cạnh a nội tiếp đường tròn (O). Tính bán kính đường tròn nội tiếp tam giác ABC. A.
r
a
3
3
B.
r
a
3
2
C.
r
a
3...
Đọc tiếp
Cho tam giác ABC đều cạnh a nội tiếp đường tròn (O). Tính bán kính đường tròn nội tiếp tam giác ABC.
A. r = a 3 3
B. r = a 3 2
C. r = a 3 6
D. r = a 2 3
Chọn đáp án C.
Gọi M là trung điểm của BC: 
Do tam giác ABC đều nên tâm đường tròn nội tiếp tam giác ABC là trọng tâm, tâm đường tròn ngoại tiếp tam giác ABC
Áp dụng định lí Pytago vào tam giác ABM ta có:

Đúng 0
Bình luận (0)
Đường tròn (O;R) nội tiếp tam giác ABC. Các tiếp tuyến với đường tròn (O) song song với các cạnh của tam giác ABC cắt từ tam giác ABC thành ba tam giác nhỏ. Gọi r1,r2,r3�1,�2,�3 lần lượt là bán kính các đường tròn nội tiếp tam giác nhỏ đó. Chứng minh rằng: r1+r2+r3r
Đọc tiếp
Đường tròn (O;R) nội tiếp tam giác ABC. Các tiếp tuyến với đường tròn (O) song song với các cạnh của tam giác ABC cắt từ tam giác ABC thành ba tam giác nhỏ. Gọi lần lượt là bán kính các đường tròn nội tiếp tam giác nhỏ đó. Chứng minh rằng:
a) Vẽ tam giác đều ABC cạnh a = 3cm.
b) Vẽ tiếp đường tròn (O; R) ngoại tiếp tam giác đều ABC. Tính R.
c) Vẽ tiếp đường tròn (O; r) nội tiếp tam giác đều ABC. Tính r.
d) Vẽ tiếp tam giác đều IJK ngoại tiếp đường tròn (O; R).
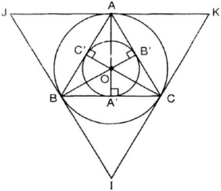
a) Vẽ tam giác đều ABC có cạnh bằng 3cm (dùng thước thẳng và compa).
+ Dựng đoạn thẳng AB = 3cm .
+Dựng cung tròn (A, 3) và cung tròn (B, 3). Hai cung tròn này cắt nhau tại điểm C.
Nối A với C, B với C ta được tam giác đều ABC cạnh 3cm.
b) * Vẽ đường tròn:
Tâm O của đường tròn ngoại tiếp tam giác đều ABC là giao điểm của ba đường trung trực.
Dựng đường trung trực của đoạn thẳng BC và CA.
Hai đường trung trực cắt nhau tại O.
Vẽ đường tròn tâm O, bán kính OA = OB = OC ta được đường tròn ngoại tiếp tam giác ABC.
* Tính bán kính đường tròn.
+ Gọi A’ là trung điểm BC ⇒ A’C = BC/2 = a/2.
và AA’ ⊥ BC
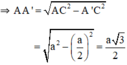
+ Do tam giác ABC là tam giác đều nên 3 đường trung trực đồng thời là ba đường trung tuyến
=> Giao điểm ba đường trung trực cũng là giao điểm ba đường trung tuyến
Suy ra O là trọng tâm tam giác ABC.
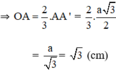
Vậy R = √3 (cm).
c) * Vẽ đường tròn:
Gọi A’; B’; C’ lần lượt là chân đường phân giác trong ứng với các góc 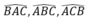
Do tam giác ABC là tam giác đều nên A’; B’; C’ đồng thời là trung điểm BC; CA; AB.
Đường tròn (O; r) là đường tròn tâm O; bán kính OA’ = OB’ = OC’.
* Tính r:
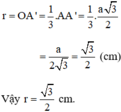
d) Vẽ các tiếp tuyến với đường tròn (O; R) tại A, B, C. Ba tiếp tuyến này cắt nhau tại I, J, K. Ta có ΔIJK là tam giác đều ngoại tiếp (O; R).
Đúng 0
Bình luận (2)
đường tròn (o;r) nội tiếp tam giác abc. Các tiếp tuyến đường tròn (o) song song với các cạnh của tam giác abc cắt từ tam giác abc thành 3 tam giác nhỏ. Gọi r1,r2,r3 lần lượt là bán kính đường tròn nội tiếp các tam giác nhỏ đó. Chứng minh M à trung điểm của en












