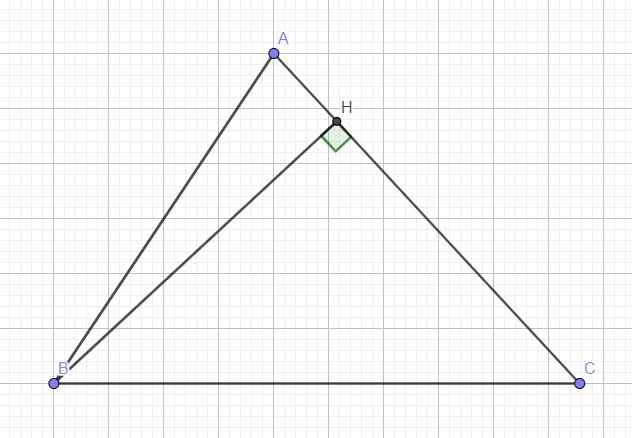
cho tam giác nhọn ABC (AB<AC)nội tiếp đường tròn (O;R).Vẽ đường kính AD vẽ AE\(\perp\)BC tại E , gọi K là giao điểm của AE với đường tròn (O;R)(K\(\ne\)A).Chứng minh rằng:
1/ AE.AD=AB.AC,S\(_{ABC}\)=\(\frac{AB.AC.BC}{4R}\)
2/ Tứ giác BKDC là hình thang cân