Thay \(AB;CD;EF;PQ\) độ dài , ta được
\(\dfrac{AB}{CD}=\dfrac{6}{7}\)
\(\dfrac{EF}{PQ}=\dfrac{18}{21}\)
Những câu hỏi liên quan
thay a va b a,b x ab,a = ab,ab
Thay các chữ cái trong phép tính = các chữ số thích hợp ( các chữ khác nhau thì thay = chữ số khác nhau)
ab,ab - a,b = 70,98
a) Cho đoạn thẳng AB. Lấy các điểm A1, A2, A3, ..., A2017 lần lượt là trung điểm của các đoạn thẳng AB, AA1, AA2, AA3, ..., AA2017Tính:M AB/AA1+ AB/AA2+ AB/AA3+ .....+ AB/AA2017b)Cho đoạn thẳng AB độ dài ko thay đổi và O là điểm tùy ý trên tia đối của tia AB. Lấy M, N lần lượt là trung điểm của đoạn thẳng OA, OB. Chứng tỏ rằng độ dài đoạn thẳng MN ko thay đổi khi điểm O thay đổi vị trí ở trên tia đối của tia AB
Đọc tiếp
a) Cho đoạn thẳng AB. Lấy các điểm A1, A2, A3, ..., A2017 lần lượt là trung điểm của các đoạn thẳng AB, AA1, AA2, AA3, ..., AA2017
Tính:M= AB/AA1+ AB/AA2+ AB/AA3+ .....+ AB/AA2017
b)Cho đoạn thẳng AB độ dài ko thay đổi và O là điểm tùy ý trên tia đối của tia AB. Lấy M, N lần lượt là trung điểm của đoạn thẳng OA, OB. Chứng tỏ rằng độ dài đoạn thẳng MN ko thay đổi khi điểm O thay đổi vị trí ở trên tia đối của tia AB
thay ab bằng chữ số ab+ba=77
a= 4 hoăc 3
b= 3 howacj 4 hiểu chư
thay 34+ 43 hoặc
43 + 34
Đúng 0
Bình luận (0)
TA có 11 x (a+b)=77 nên a+b=7 suy ra (a,b)=(1,6)(2,7)(3,4)(5,2)(6,1)(0,7),(7,0)
Đúng 0
Bình luận (0)
Tam giác ABC vuông tại A có đường cao là AD (D ∈ BC). Từ D, kẻ DE vuông góc với AB (E ∈ AB) và DF vuông góc với AC (F ∈ AC).Hỏi rằng, khi độ dài các cạnh AB, AC thay đổi thì tổng
A
E
A
B
+
A
F
A
C
có thay đổi hay không? Vì sao?
Đọc tiếp
Tam giác ABC vuông tại A có đường cao là AD (D ∈ BC). Từ D, kẻ DE vuông góc với AB (E ∈ AB) và DF vuông góc với AC (F ∈ AC).
Hỏi rằng, khi độ dài các cạnh AB, AC thay đổi thì tổng A E A B + A F A C có thay đổi hay không? Vì sao?
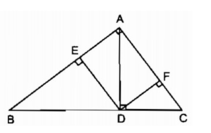
DE và CA cùng vuông góc với AB, do đó
DE // AC.
Theo định lí Ta-lét, ta có:
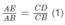
Tương tự, ta có: DF // AB, do đó:
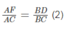
Cộng các vế tương ứng của (1) và (2), ta có:
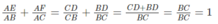
Tổng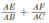 
không thay đổi vì luôn có giá trị bằng 1.
Vậy : Khi độ dài cạnh góc vuông AB, AC của tam giác vuông ABC thay đổi thì tổng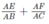 
luôn luôn không thay đổi. Tổng đó luôn có giá trị bằng 1.
Đúng 0
Bình luận (0)
thay các chữ ab bằng các số thích hợp aa.ab=abb+ab
thay các chữ a, b ( a khác b ) sao cho aa + ab = abb + ab ( aa, ab, abb có gạch trên đầu)
Cho điểm M nằm bên trong (O;R). Qua M kẻ 2 dây AB và CD vuông góc với nhau. CMR: Nếu M cố định, 2 dây AB và CD thay đổi nhưng vẫn vuông góc với nhau thì AB2 + CD2 luôn không thay đổi.
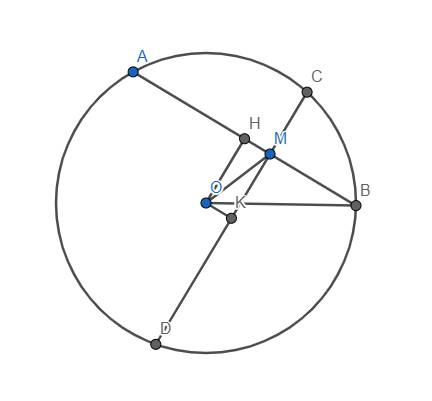
Hạ \(OH\perp AB\), \(OK\perp CD\). Dễ thấy tứ giác OHMK là hình chữ nhật \(\Rightarrow HK=OM\)
Lại có \(AB^2=4HB^2=4\left(OB^2-OH^2\right)=4R^2-4OH^2\) (1)
và \(CD^2=4CK^2=4\left(OC^2-OK^2\right)=4R^2-4OK^2\) (2)
Từ (1) và (2), suy ra \(AB^2+CD^2=8R^2-4\left(OH^2+OK^2\right)\) \(=8R^2-4HK^2=8R^2-4OM^2\) không đổi, đpcm.
Đúng 1
Bình luận (0)
Cho hình thang ABCD có AB//CD, AB<CD, M thuộc AB, E và F lần lượt là trung điểm của AC và BD, H đối xứng với M qua E, K đối xứng M qua F CM
1) D, K, H, C thẳng hàng
2) CM HK không thay đổi, IM thay đổi trên AB
xét tg AMCH có: E là t/đ của của MH và AC => tg AMCH là hbh=> AM//HC
xét tg BMDK có: F là t/đ của MK và BD => tg BMDK là hbh => BM//DK
Mà M thuộc AB (gt) => AB // HC//DK. (1)
Mặt khác : AB // DC (2)
Từ (1),(2)=> D,K,H,C thẳng hàng (tiên đề Ơ -clit)
b) do tg AMCH là hbh (c/m câu a)=> AM=CH (3)
Do tg BMDK là hbh (.................)=> BM=DK (4)
Từ(3),(4)=> AM+BM=CH+DK
=> AB=CH+DK (5)
Mặt khác: Dk+KH+HC=DC=> KH=DC-(DK+HC) (6)
Từ (5),(6),=> HK=DC-AB
Mà hthang ABCD cố định nên AB và DC ko đổi => DC-AB ko đổi => HK ko đổi
Vậy khi M di chuyển trên AB thì độ dài HK ko đổi
Đúng 0
Bình luận (0)
tam giác ABC vuông tại A đường cao AH . từ H kẻ HE vuông góc vs AB và HF vuông góc vs AC . hỏi khi độ dài AB,AC thay đổi thì AE/AB+AF/AC có thay đổi ko?
