Tham khảo

nối đường chéo AC
Trong ∆ABC ta có
E là trung điểm của AB
F là trung điểm của BC
Nên EF là đường trung bình của ∆ABC
EF//=1/2AC(1)
(Sd tính chất của đng trung bình)
Chứng minh tương tự với ∆ADC
=> HG//=1/2AC(2)
Từ (1) và(2) suy ra EF//=HG
Vậy tứ giác EFGHlaf hình bình hành
Vì có một cặp đối song song và bằng nhau

Tự vẽ hình :)

t/g ABC có :

AE = EB

BF = FC

\(\Rightarrow\)EF - đường trung bình của tam giác ABC

\(\Rightarrow\)\(EF\)//   \(AC\)\(,\)\(EF=\frac{AC}{2}\left(1\right)\)

t/g ADC có :

AH = HD

CG = GD

\(\Rightarrow\)HG - đường trung bình của tam giác ADC

\(\Rightarrow\)\(HG\)//   \(AC\)\(,\)\(HG=\frac{AC}{2}\)\(\left(2\right)\)

Từ ( 1 ) và ( 2 ) \(\Leftrightarrow\)EF // HG , EF = HG

Vì tứ giác EFGH có 2 cạnh đối song song và bằng nhau

\(\Rightarrow\)EFGH - hình bình hành ( đpcm )

xem lại đề bài nhé bạn :)

ghi cái đề bài cũng sai :v

Em tự vẽ hình nhé. Ý sau cô nói rõ yêu cầu hơn là chứng minh hình bình hành MNPQ có chu vi bằng tổng độ dài hai đường chéo của tứ giác ABCD.

Xét tứ giác EFMN có OF = ON; OE = OM nên nó là hình bình hành (Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường)

Vậy thì MN // EF // AC và MN = EF = AC / 2 (Vì EF là đường trung bình tam giác BAC).

Hoàn toàn tương tự: QP // GH // AC và QP = GH = AC/2.

Vậy MNPQ là hình bình hành (Cặp cạnh đối song song và bằng nhau).

Khi đó ta có:

 \(p_{MNPQ}=PQ+PN+NM+MQ=\left(PQ+MN\right)+\left(MQ+PN\right)=AC+BD.\)

Vậy ta đã chứng minh xong bài toán.

Cô ơi em ko hiểu.Theo em thì ta phải cm MN//=AC và PQ//=AC

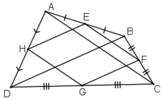
+ E là trung điểm AB, F là trung điểm BC

⇒ EF là đường trung bình của tam giác ABC

⇒ EF // AC và EF = AC/2

+ H là trung điểm AD, G là trung điểm CD

⇒ HG là đường trung bình của tam giác ACD

⇒ HG // AC và HG = AC/2.

+ Ta có:

EF //AC, HG//AC ⇒ EF // HG.

EF = AC/2; HG = AC/2 ⇒ EF = HG

⇒ tứ giác EFGH là hình bình hành.

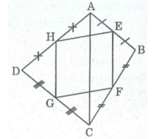
Nối đường chéo AC.

Trong ∆ ABC ta có:

E là trung điểm của AB (gt)

F là trung điểm của BC (gt)

Nên EF là đường trung bình của  ∆ ABC

⇒EF//AC và EF = 1/2 AC

(tính chất đường trung hình tam giác) (1)

Trong  ∆ ADC ta có:

H là trung điểm của AD (gt)

G là trung điểm của DC (gt)

Nên HG là đường trung bình của ∆ ADC

⇒ HG // AC và HG = 1/2 AC (tính chất đường trung bình tam giác) (2)

Từ (1) và (2) suy ra: EF // HG và EF = HG

Vậy tứ giác EFGH là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau).

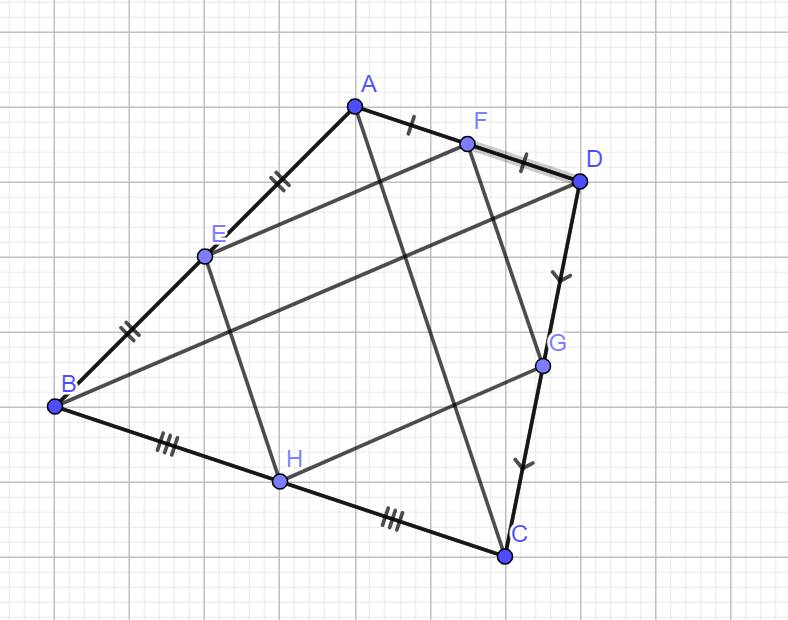
E là trung điểm AB, F là trung điểm BC

⇒ EF là đường trung bình của tam giác ABC

⇒ EF // AC và EF = AC/2

+ H là trung điểm AD, G là trung điểm CD

⇒ HG là đường trung bình của tam giác ACD

⇒ HG // AC và HG = AC/2.

+ Ta có:

EF //AC, HG//AC ⇒ EF // HG.

EF = AC/2; HG = AC/2 ⇒ EF = HG

⇒ tứ giác EFGH là hình bình hành.

Em xem lại đề, em ghi sai đề rồi. Còn bạn Thiện Nhân giải ở dưới thì vẽ hình sai!

- Vì ta nối DB thì sẽ có HE và GF là đường tb của tam giác ADB và DCB => GF//HE vì cùng // với DB và bằng 1/2 DB (1)
- Nối AC thì sẽ có HG và EF là đường tb của tam giác DCA và BAC => EF//HG vì cùng //AC và bằng 1/2 AC (2)
Từ (1) và (2) => tứ giác HEFG là HBH (có các cặp cạnh // và bằng nhau từng đôi một)

=>Hình đó là hình bình hành

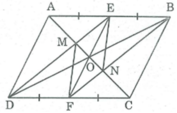
Xét tứ giác DEBF, ta có:

AB // CD (gt) hay DF // EB

EB = 1/2 AB (gt)

DF = 1/2 CD (gt)

Suy ra: EB = DF

Tứ giác DEBF là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau).

Trả lời :

+ E là trung điểm AB, F là trung điểm BC

⇒ EF là đường trung bình của tam giác ABC

⇒ EF // AC và EF = \(\frac{AC}{2}\)

+ H là trung điểm AD, G là trung điểm CD

⇒ HG là đường trung bình của tam giác ACD

⇒ HG // AC và HG = \(\frac{AC}{2}\).

+ Ta có:

EF // AC, HG//AC ⇒ EF // HG.

EF = \(\frac{AC}{2}\); HG = \(\frac{AC}{2}\) ⇒ EF = HG

⇒ Tứ giác EFGH là hình bình hành.

ai biet

sdfvbnm,.

À mà bạn tự vẽ hình nhé

Kẻ đường chéo AC(BD cũng được)

Xét tam giác ABC có: AE=EB:BF=CF

Do đó EF là đường trung bình của tam giác ABC

=>EF//AC:EF=1/2AC (1)

TTự: Xét tam giác ADC có: CG=DG:AH=DH

Do đó GH là đường trung bình của tam giác ADC

=>GH//AC:GH=1/2AC (2)

Từ (1) và (2) suy ra EF//GH:EF=GH

Vậy tứ giác EFGH là hình bình hành

Thấy đúng thì chia sẻ nha :D

hình bình hành áp dụng tính chất đương trung bình nhá