Bài 3: Cho tam giác ABC vuông tại B. Trên cạnh AC lấy điểm E sao cho AB = AE. Gọi I là trung điểm của BE; K là giao điểm của AI và BC. Trang 4 a) Chứng minh: tg ABI = tg AEI b) Chứng minh: AI ⊥ BE c) Tính số đo góc KEA

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A, AB<AC đường cao AH. Lấy điểm E trên cạnh AC sao cho AE=AB. Gọi I là trung điểm của BE. Tính số đo góc IHA.
Bạn xem tại đây
http://olm.vn/hoi-dap/question/234367.html
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A (AB < AC). Kẻ tia phân giác của góc ABC cắt AC tại D. Trên cạnh BC lấy điểm E sao cho: BE = AB. 1) Chứng minh rằng: ∆ABD = ∆EBD; 2) Gọi giao điểm của BD và AE là I. Hỏi I có là trung điểm của AE không? Vì sao? 3) Kéo dài ED cắt AB tại K. Chứng minh: AK = EC và AE // KC.
b, Vì ∆ABD=∆EBD
=>BAD=BED=90°
=>DE//BC
Ta có AH vuông góc BC
DE vuông góc BC
=>AH//DE(đpcm)
c,Đó AH//DE (đpcm)
=>AH//DK.
Cho tam giác ABC nhọn có AB<AC. Trên cạnh BC lấy điểm E sao cho AB=AE, gọi H là trung điểm của BE.
1. Chứng minh: tam giác ABH = tam giác AEH
2. Chứng minh AH vuông góc BE 3. Trên tia AH lấy điểm F sao cho AH = HF. Kẻ tia Ax // BC, trên Ax lấy điểm I sao cho AI = BE ( I cùng phía B so với đường thẳng AH )
a) Chứng minh: BF=AE
b) Chứng minh: 3 điểm I, B, F thẳng hàng
1: Xét ΔABH và ΔAEH có
AB=AE
BH=EH
AH chung
Do đó: ΔABH=ΔAEH
Đúng 2
Bình luận (0)
1: Xét ΔABH và ΔAEH có
AB=AE
BH=EH
AH chung
Do đó: ΔABH=ΔAEH
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A (AB<AC), đường cao AH. Trên cạnh AC lấy điểm E sao cho AB=AE. Gọi M là trung điểm của BE. Chứng minh rằng HM là phân giác góc AHC.
Bài 1: Cho tam giác ABC, trên cạnh AB lấy 2 điểm D và F sao cho AD DF FB. Các trung tuyến AE, BG của tam giác ABC lần lượt cắt CD, CF tại H và K.a) CMR: GH, EK, AB cắt nhau tại 1 điểmb) CMR: AB 4HKBài 2: Cho tam giác ABC có BD và CE là phân giác, cắt nhau tại I. Gọi S là trung điểm BC, biết BI 2IS.a) CMR: tam giác ABC vuôngb) CMR: ID / IB CD / CBBài 3: Cho tam giác ABC vuông cân tại A. Trên cạnh AB và AC lần lượt lấy các điểm D và E sao cho AD AE. Qua A và D, kẻ các đường thẳng vuông góc v...
Đọc tiếp
Bài 1: Cho tam giác ABC, trên cạnh AB lấy 2 điểm D và F sao cho AD = DF = FB. Các trung tuyến AE, BG của tam giác ABC lần lượt cắt CD, CF tại H và K.
a) CMR: GH, EK, AB cắt nhau tại 1 điểm
b) CMR: AB = 4HK
Bài 2: Cho tam giác ABC có BD và CE là phân giác, cắt nhau tại I. Gọi S là trung điểm BC, biết BI = 2IS.
a) CMR: tam giác ABC vuông
b) CMR: ID / IB = CD / CB
Bài 3: Cho tam giác ABC vuông cân tại A. Trên cạnh AB và AC lần lượt lấy các điểm D và E sao cho AD = AE. Qua A và D, kẻ các đường thẳng vuông góc với BE cắt BC thứ tự tại S và T. CMR: S là trung điểm của TC
Cho tam giác ABC vuông cân đỉnh A. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E, sao cho ADAE. Gọi I là giao điểm của BE và CD, chứng minh:a, BECDb, tam giác BID tam giác CIEc, AI là trung trực của đoạn thẳng BCd, Qua D vẽ đường thẳng vuông góc với BE, cắt BE ở K, cắt AC ở H, chứng minh: A là trung điểm của đoạn thẳng HCGiúp mik với mik đang cần gấp!!!!
Đọc tiếp
Cho tam giác ABC vuông cân đỉnh A. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E, sao cho AD=AE. Gọi I là giao điểm của BE và CD, chứng minh:
a, BE=CD
b, tam giác BID = tam giác CIE
c, AI là trung trực của đoạn thẳng BC
d, Qua D vẽ đường thẳng vuông góc với BE, cắt BE ở K, cắt AC ở H, chứng minh: A là trung điểm của đoạn thẳng HC
Giúp mik với mik đang cần gấp!!!!
a) Xét ΔABE vuông tại A và ΔACD vuông tại A có
AB=AC(ΔABC vuông cân tại A)
AE=AD(gt)
Do đó: ΔABE=ΔACD(cạnh huyền-cạnh góc vuông)
Suy ra: BE=CD(Hai cạnh tương ứng)
Đúng 0
Bình luận (0)
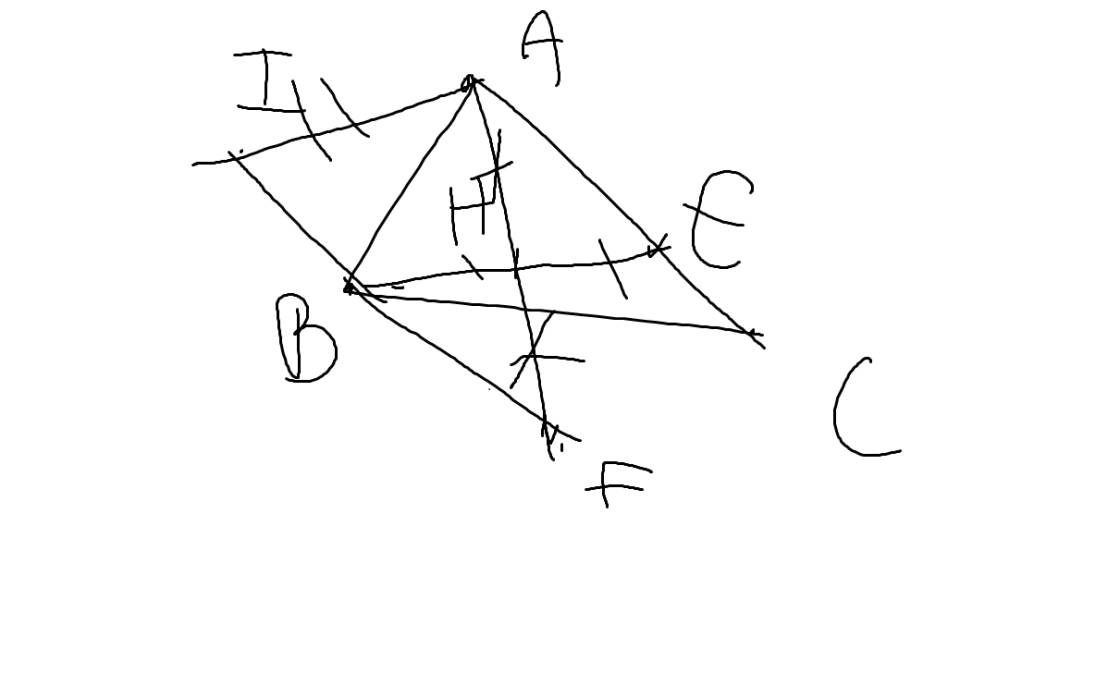
Cho tam giác ABC nhọn có ABAC. Trên cạnh AC lấy E sao cho ABAE. Gọi H là trung điểm BE. 1) Chứng minh tam giác ABHAEH (c.c.c) 2) Chứng minh AH vuông góc BE 3) Trên AH lấy điểm F sao AHHF. Kẻ Ax // BC. Trên Ax lấy I sao AIBE (I cùng phía với AH). Chứng minh rằng: a) Chứng minh BFAE b) Chứng minh 3 điểm I, B, F thẳng hàng ( kẻ hình nữa nhé ) cảm ơn các bạn nhiều , lm nhanh nhất có thể giúp mik nhé
Đọc tiếp
Cho tam giác ABC nhọn có AB<AC. Trên cạnh AC lấy E sao cho AB=AE. Gọi H là trung điểm BE. 1) Chứng minh tam giác ABH=AEH (c.c.c) 2) Chứng minh AH vuông góc BE 3) Trên AH lấy điểm F sao AH=HF. Kẻ Ax // BC. Trên Ax lấy I sao AI=BE (I cùng phía với AH). Chứng minh rằng: a) Chứng minh BF=AE b) Chứng minh 3 điểm I, B, F thẳng hàng ( kẻ hình nữa nhé )
cảm ơn các bạn nhiều , lm nhanh nhất có thể giúp mik nhé ![]()
1: Xét ΔABH và ΔAEH có
AB=AE
BH=EH
AH chung
Do đó: ΔAHB=ΔAHE
2: ΔAHB=ΔAHE
=>\(\widehat{AHB}=\widehat{AHE}\)
mà \(\widehat{AHB}+\widehat{AHE}=180^0\)(hai góc kề bù)
nên \(\widehat{AHB}=\widehat{AHE}=\dfrac{180^0}{2}=90^0\)
=>AH\(\perp\)BE
3: Sửa đề: Kẻ tia Ax//BE, trên Ax lấy I sao cho AI=BE(I và B nằm cùng phía so với AH)
a: Xét tứ giác ABFE có
H là trung điểm chung của AF và BE
=>ABFE là hình bình hành
=>BF=AE và BF//AE
b:
Xét tứ giác AEBI có
AI//BE
AI=BE
Do đó: AEBI là hình bình hành
=>BI//AE
Ta có: BF//AE
BI//AE
BI,BF có điểm chung là B
Do đó: F,B,I thẳng hàng
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại a . Trên tia đối của tia ab lấy điểm d sao cho ab=ad
a) CM tam giác ABC = tam giác adc
b) trên tia đối của tia ac lấy điểm e sao cho ac = ae . Cm dc//be
C) lấy điểm i là trung điểm đc . Cm be = 2.ai
a) chứng minh \(\Delta ABC=\Delta ADC\)
xét 2 tam giác vuông ABC và ADC:
có AC: cạnh chung
AD=AB (gia thiết)
=> \(\Delta ABC=\Delta ADC\) (2cgv)
b) chứng minh DC//BE
xét tứ giác BEDC có 2 đường chéo BD và EC cắt nhau tại trung điểm A của mỗi đường => tứ giác BEDC là hình bình hành => DC//BE
c) chứng minh BE = 2AI
ta có BEDC là hình bình hành => BE=DC
lại có tam giác DAC vuông tại A => đường trung tuyến AI bằng một nửa cạnh huyền, tức là \(AI=\dfrac{1}{2}DC\) hay \(DC=2.AI\) hay \(BE=2.AI\)
chúc em học tốt
Đúng 1
Bình luận (0)
Cậu tự vẽ hình nhé.
a, Xét \(\Delta ABC\) vuông tại A và \(\Delta ADC\) vuông tại A có:
AB = AD(gt)
AC chung
\(\Rightarrow\Delta ABC=\Delta ADC\left(ch-cgv\right)\)
b, Ta có \(DB\perp EC\) tại \(A\)
mà \(DA=AB\left(gt\right)\)
\(AE=AC\left(gt\right)\)
\(\Rightarrow\) Tứ giác DCBE là hình thoi ( 2 đường chéo vuông góc với nhau và cắt nhau tại trung điểm mỗi đường )
\(\Rightarrow DC//BE\) ( tính chất hình thoi )
c, Xét \(\Delta DAC\) vuông tại A có:
I là trung điểm của DC
\(\Rightarrow AI=DI=IC=\dfrac{1}{2}DC\)
\(\Rightarrow2AI=DC\)
Lại có DC = EB ( DCBE là hình thoi )
\(\Rightarrow2AI=BE\)
Đúng 1
Bình luận (0)
Bài 1.13: Cho tam giác ABC vuông tại A. Gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MA MD.a) Chứng minh: AB CDb) Chứng minh: BD // ACc) Tính số đo góc ABD Bài 1.14: Cho tam giác ABC, AB AC. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho AD AE. Gọi M là giao điểm của BE và CD. Chứng minh rằng:a) BE CDb) ∆BMD ∆CNEc) AM là tia phân giác của góc BAC
Đọc tiếp
Bài 1.13: Cho tam giác ABC vuông tại A. Gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MA = MD.
a) Chứng minh: AB = CD
b) Chứng minh: BD // AC
c) Tính số đo góc ABD
Bài 1.14: Cho tam giác ABC, AB = AC. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho AD = AE. Gọi M là giao điểm của BE và CD. Chứng minh rằng:
a) BE = CD
b) ∆BMD = ∆CNE
c) AM là tia phân giác của góc BAC


















