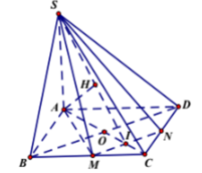
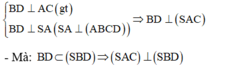Cho hình vuông ABCD có M, N lần lượt là trung điểm của BC,CD ; H là giao điểm của AM và BN . Xác định tọa độ các đỉnh của hình vuông biết AB: x-y+4=0 . d(H,AB) = \(\dfrac{8\sqrt{2}}{5}\) , điểm N thuộc đường thẳng d: x-2y-6=0 và N có hoành độ dương

Những câu hỏi liên quan
Cho hình vuông ABCD có cạnh bằng 2a. Gọi M, N lần lượt là trung điểm của BC, CD. Tính cos(MAN).
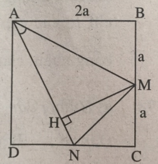
Kẻ đường cao MH của tam giác cân AMN. Ta có sin ∠ (NAM) = HM/AM và diện tích tam giác AMN là S A M N = 1/2AN.MH = 1/2AN.AM.sin(NAM) = 1/2 A N 2 .sin(NAM) = 1/2( A D 2 + D N 2 ). sin(NAM) = ( 5 a 2 )/2 sin(NAM).
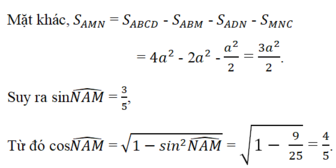
Đúng 1
Bình luận (0)
Cho hình vuông ABCD có M và N lần lượt là trung điểm của BC và CD. Tính góc MAN ?
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, SA ⊥ (ABCD) và S A = a 15 Gọi M, N lần lượt là trung điểm của BC và CD: Tính góc giữa SM và (ABCD).
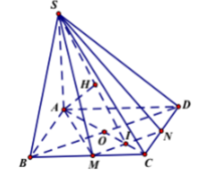
AM là hình chiếu của SM trên (ABCD).
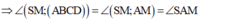
- Xét tam giác vuông ABM ta có: 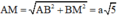
- Xét tam giác vuông SAM ta có: 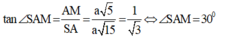
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, SA ⊥ (ABCD) và S A = a 15 Gọi M, N lần lượt là trung điểm của BC và CD: Chứng minh (SAC) ⊥ (SBD).
Cho hình vuông ABCD có cạnh dài 20cm. Các điểm M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Ta có hình thoi MNPQ. Diện tích của hình thoi là.
MP=(AD+BC)/2=20cm
NQ=(AB+CD)/2=20cm
S MNPQ=1/2*20*20=200cm2
Đúng 0
Bình luận (0)
Cho hình vuông ABCD . gọi M ,N lần lượt là trung điểm của BC và CD. Tính cos góc MAN
Vì \(\tan MAB=\frac{MB}{AB}=\frac{1}{2}\Rightarrow\widehat{MAB}=26,5°\)Tương tự có \(\widehat{NAD}=26,5°\)
\(\Rightarrow\widehat{MAN}=37°\Rightarrow\cos MAN=\cos37\approx0,79\)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, SA ⊥ (ABCD) và S A = a 15 Gọi M, N lần lượt là trung điểm của BC và CD: Tính khoảng cách từ điểm C đến mặt phẳng (SMN)?
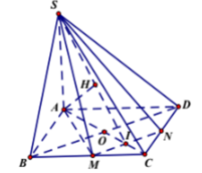
Gọi I = AC ∩ MN ⇒ I là trung điểm của OC, ta có:
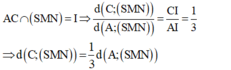
- Ta có: MN// BD mà BD ⊥ (SAC)(cmt) ⇒ MN ⊥ (SAC).
- Trong (SAC) kẻ AH ⊥ SI (H ∈ SI) ⇒ MN ⊥ AH.
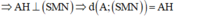
- Ta có:
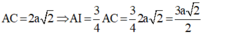
- Xét tam giác vuông SAI ta có:
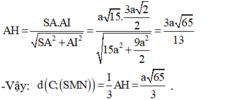
Đúng 0
Bình luận (0)
cho hình vuông ABCD có cạnh bằng 8cm. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Hãy tìm diện tích của hình vuông MNPQ.
Cho hình thang ABCD với đáy BC = 2AD. Gọi M, N, P, Q lần lượt là trung điểm của BC, MC, CD, AB và E là điểm thỏa mãn veto BN = vecto QE. Xác định vị trí điểm E Cho hình thang ABCD với đáy BC = 2AD. Gọi M, N, P, Q lần lượt là trung điểm của BC, MC, CD, AB và E là điểm thỏa mãn veto BN = vecto QE. Xác định vị trí điểm E
Xét hình thang ADCB có
Q,P lần lượt là trung điểm của AB,DC
=>QP là đường trung bình của hình thang ADCB
=>QP//AD//BC và \(QP=\dfrac{AD+BC}{2}=\dfrac{\dfrac{BC}{2}+BC}{2}=\dfrac{3}{4}BC\)
Ta có: M là trung điểm của BC
=>\(BM=MC=\dfrac{BC}{2}\)
Ta có: N là trung điểm của MC
=>\(MN=NC=\dfrac{MC}{2}=\dfrac{BC}{4}\)
BM+MN=BN
=>\(BN=\dfrac{1}{4}BC+\dfrac{1}{2}BC=\dfrac{3}{4}BC\)
=>QP=BN
Ta có: QP//BN
QP=BN
Do đó: \(\overrightarrow{QP}=\overrightarrow{BN}\)
=>Điểm E trùng với điểm P
Đúng 2
Bình luận (0)
Cho hình vuông ABCD có cạnh bằng 4cm và M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, AD. Hãy tính tổng chu vi của tất cả các hình vuông?
có 16 chí mấy ! có một hình vuông không mà
Đúng 0
Bình luận (0)