Cho hình bình hành ABCD, điểm P trên AB. Gọi M,N là các trung điểm của AD,BC;E,F lần lượt là điểm đối xứng của P qua M,N . Chứng minh rằng:
a) E,F thuộc đường thẳng CD
b) E,F=2CD
Cho hình bình hành ABCD. Gọi O là giao điểm của hai đường thẳng AC và BD. Qua điểm O vẽ đường thẳng song song với AB cắt hai cạnh AD, BC lần lượt tại M, N. Trên AB, CD lần lượt lấy các điểm P, Q sao cho AB=CQ. Gọi I là giao điểm của AC và PQ. Chứng minh:
a) Các tứ giác AMNB, APCQ là hình bình hành
b) Ba điểm M, N, I thẳng hàng
c) Ba đường thẳng AC, MN, PQ đồng quy
( vẽ hình giúp mink lun nhe ^-^)
a: Xét tứ giác AMNB có
AB//MN
AM//BN
Do đó: AMNB là hình bình hành
Hình thang ABCD (AB//CD) có DC=2AB .Gọi M,N,P,Q là trung điểm của các cạnh AB, BC,CD,DA
1) c/m các tứ giác ABPQ, MNPQ là hình bình hành
2) Tìm điều kiện của hình thang ABCDđể MNPQ là hình thoi
3) Gọi E là giao đimể của BD và AP . C/m ba điểm Q,N,E thẳng hàng
câu c:
-chứng minh ABPD là hình bình hành suy ra:Elà trung điểm của AP
-Suy ra QElà đường trung bình tam giác APD , do đó :QE // PD (1)
-Mà QN là đường trung binh hình thang ABCD suy ra: QN//CD (2)
-Từ (1) và (2) suy ra :Q,N,E thẳng hành (theo tiên đề ơ-cơlit)
cho hình bình hành ABCD. gọi E là trung điểm cùa AD, F là trung điểm của BC . chứng minh rằng BE=DF
ABCD là hình bình hành \(\Rightarrow\) AB = CD; góc A = góc C; AD = BC
E là trung điểm của AD \(\Rightarrow\) AE = \(\frac{AD}{2}\)
F là trung điểm của BC \(\Rightarrow\) FC = \(\frac{BC}{2}\)
mà AD = BC (cmt)
nên AE = FC
Xét \(\Delta\) ABE và \(\Delta\) CDF có
góc A = góc C (cmt)
AE = FC (cmt)
AB = CD (cmt)
\(\Rightarrow\) tam giác ABE = tam giác CDF (c.g.c)
\(\Rightarrow\) BE = DF
1.Cho hình bình hành ABCD, AC cắt BD ở O. Trên đường chéo AC lấy E,F để AE=EF=FC. DE cắt AB ở M, BF cắt Cd ở N. CMR:
a) BFDE là hình bình hành
b) O là trung điểm của MN
2. Cho hình bình hành ABCD. Gọi E,F lần lượt là trung điểm của AB, AD. Đường thẳng EF cắt các tia CD,CB ở H và K. CMR:
a) FH = EK
b) tan giác CEF và tam giác HCK có cùng trọng tâm
1. Cho hình bình hành ABCD có AB= 2AD. Gọi M, N theo tứ tự là trung điểm của các cạnh AB, CD. Gọi P và Q lần lượt là giao điểm của BN với CM và của AN với DM
a. Tứ giác AMND là hình gì? Vì sao?
b. Chứng minh: tứ giác MPNQ là hình chữ nhật
c. Tìm điều kiện của tứ giác ABCD để MPNQ là hình vuông
d. Chứng minh: bốn đường thẳng AC, BD, MN, QP đồng qui
2. Cho hình bình hành ABCD. Kẻ AN, CM vuông góc với BD, N và M thuộc BD
a. Chứng minh DN = BM
b. Chứng minh Tứ giác ANCM là hình bình hành
c. Gọi K là điểm đối xứng với A qua N. Tứ giác DKCB là hình gì? Vì sao?
d. Tia AM cắt tia KC tại P. Chứng minh các đường thẳng AC, PN, KM đồng qui
Bài 1: Tam giác ABC có AM, BN là các trung tuyến, G là trọng tâm. Gọi E và F lần
lượt là trung điểm của GB và GA. Gọi I là điểm đối xứng với G qua M.
a) Chứng minh BICG và MNFE là hình bình hành.
b) Để MNFE là hình chữ nhật thì cần có thêm điều kiện gì cho tam giác ABC ?
c) Khi BICG là hình thoi, hãy chứng minh tam giác ABC cân tại A.
Bài 2: Cho hình bình hành ABCD. Gọi E là điểm đối xứng của A qua trung điểm M
của BC.
a) Chứng minh ABEC là hình bình hành và D, E, C thẳng hàng.
b) Tam giác ABC phải có điều kiện gì thì ABEC trở thành hình thoi.
a, xét tứ giác BICG có :
M là trung điểm cuả BC do AM là trung tuyến (gt)
M là trung điểm của GI do I đx G qua M (gt)
=> BICG là hình bình hành (dh)
+ G là trọng tâm của tam giác ABC (gt)
=> GM = AG/2 và GN = BG/2 (đl)
E; F lần lượt là trung điểm của GB; GA (gt) => FG = AG/2 và GE = BG/2 (tc)
=> FG = GM và GN = GE
=> G là trung điểm của FM và EN
=> MNFE là hình bình hành (dh)
b, MNFE là hình bình hành (câu a)
để MNFE là hình chữ nhật
<=> NE = FM
có : NE = 2/3BN và FM = 2/3AM
<=> AM = BN mà AM và BN là trung tuyến của tam giác ABC (Gt)
<=> tam giác ABC cân tại C (đl)
c, khi BICG là hình thoi
=> BG = CG
BG và AG là trung tuyến => CG là trung tuyến
=> tam giác ABC cân tại A
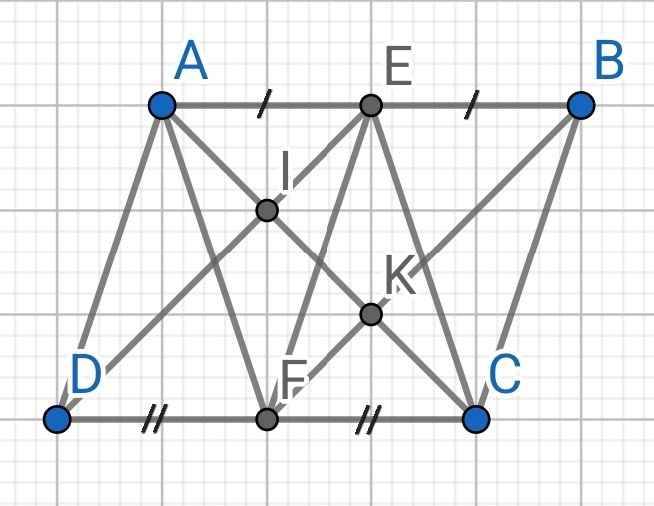
cho hình bình hành ABCD gọi EF lần lược là trung điểm của AB và CD , AF cắt DE tại M và EC cắt BF tại N . Chứng minh các tứ giác sau đây là hình bình hành :
A) AEFD
B) EBCF
C) AECF
D)EBFD
E ) chứng minh M là chung điểm của AF và DE, N là chung diểm của EC và FB
 a) Do ABCD là hình bình hành (gt)
a) Do ABCD là hình bình hành (gt)
⇒ AB = CD (1)
Do E là trung điểm AB (gt)
⇒ AE = BE = AB : 2 (2)
Do F là trung điểm CD (gt)
⇒ CF = DF = CD : 2 (3)
Từ (1), (2) và (3)
⇒ AE = BE = CF = DF
Do ABCD là hình bình hành (gt)
⇒ AB // CD
⇒ AE // CF
Tứ giác AECF có:
AE // CF (cmt)
AE = CF (cmt)
⇒ AECF là hình bình hành
b) Do AB // CD (cmt)
⇒ BE // DF
Tứ giác BEDF có:
BE // DF (cmt)
BE = DF (cmt)
⇒ BEDF là hình bình hành
⇒ BF // DE
⇒ BK // EI và KF // DI
∆CDI có:
F là trung điểm CD (gt)
KF // DI (cmt)
⇒ K là trung điểm của CI
⇒ CK = IK (4)
∆ABK có:
E là trung điểm của AB (gt)
BK // EI (cmt)
⇒ I là trung điểm của AK
⇒ AI = IK (5)
Từ (4) và (5)
⇒ AI = IK = KC
Bài 1 Cho hình bình hành ABCD. Có góc A=60 độ, AB=BC. Cm AC= A 969 9 t của 3
Bài 2. Cho tam giác ABC cân tại A. D thuộc AB, E thuộc AC. Sao cho AD=CE. I là trung điểm DE. AI giao BC tại K. Cm từ giác ADKE là hình bình hành
Bài 3. Cho tứ giatc ABCD. Trên AB lấy điểm E,, F sao cho AE=EF=FB. Trên CD lấy điểm G, H sao cho DG=HG=HC. Lấy M, I, N, K lần lượt là trung điểm AD, EG, FH, BC. chứng minh
a) tứ giác MNEG là hình bình hành
b) 4 điểm M,I,N,K thẳng hàng
Giúp đi, mai đi học rồi, cả 3 câu nhá