cho tam giác ABC kẻ BE vuông góc với AC ; CF vuông góc AB gọi O là giao điểm của BE và CF biết OC=AB tính ACB

Những câu hỏi liên quan
cho tam giác ABC, có AB = AC, kẻ bE vuông góc với AC, CD vuông góc với AB. Gọi O là giao điểm của BE và CD. CMR : a) tam giác ABC = tam giác AEB, b) AO là phân giác của BAC
a: Xét ΔAEB vuông tại E và ΔADC vuông tại D có
AB=AC
\(\widehat{A}\) chung
Do đó: ΔAEB=ΔADC
Đúng 1
Bình luận (1)
Cho tam giác ABC. Kẻ BE vuông góc với AC, kẻ CF vuông góc với AB( E thuộc AC, F thuộc AB). Gọi O là giao điểm của BE, CF. Biết OC=AB. Tính góc ACB
Xét Δ vuông ABE và Δ vuông OCE có:
AB=OC (giả thiết)
gócABE=gócOCE (cùng phụ với gócA)
⇒Δ vuông ABE=Δ vuông OCE (ch-gn)
⇒BE=CE ⇒ΔBEC vuông cân tại đỉnh E
⇒gócACB=\(\dfrac{180độ-gócE}{2}\)=\(\dfrac{180độ-90độ}{2}\)=45độ
Vậy....
Đúng 2
Bình luận (0)
Cho tam giác abc cân tại b . Kẻ bh vuông góc ac (h thuộc ac) Cm a) tam giác abc = tam giác cbh b) cho bh = 4 cm, ac = 6 cm . Tính bc =? c) kẻ he vuông góc ab, hf vuông góc bc . Cm be= bf
cho tam giác ABC có góc A=90 độ, AB<AC. Kẻ đường cao AH vuông góc với BC. Kẻ AD là phân giác góc HAC. Kẻ BE là đường phân giác góc ABC. CMR BE vuông góc với AD
cac ban oi giup minh nhe
Goi F la giao diem cua BE va AH, I la giao diem cua BE va AD
ta co: goc ABC+ goc ACB=90 ( tam giac ABC vuong tai A)
goc HAC+ goc ACB=90 ( tam giac AHC vuong tai H)
===> goc ABC= goc HAC
ta co : goc HAD=1/2 goc HAC ( AD la tia p/g goc HAC)
goc FBH=1/2 goc ABC ( BE la tia p/g goc ABC )
goc ABC= goc HAC ( cmt)
--> goc HAD= goc FBH
ta co: goc BFH+ goc FBH =90 ( tam giac FBH vuong tai H)
goc FBH= goc HAD ( cmt)
goc BFH= goc AFI ( 2 goc doi dinh)
===> goc HAD+ goc AFI =90 hay goc FAI+ goc AFI=90
xet tam giac AFI ta co: goc AFI+ gic FAI+ goc AIF=180 ( tong 3 goc trong tamgiac )
ma goc AFI+ goc FAI =90 ( cmt )
nen 90+ goc AIF =180
--> goc AIF =180-90=90
--> AI vuong goc FI hay BE vuong goc AD tai I
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A, BE là tia phân giác của góc ABC(E thuộc AC). Kẻ ED vuông góc với BC (Dthuộc BC) a, chứng minh tam giác ABE=tam giác DBE và AE
Xét ΔABE vuông tại A và ΔDBE vuông tại D có
BE chung
góc ABE=góc DBE
Do đó: ΔABE=ΔDBE
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông ở A có góc B bằng 60 độ . Tia phân giác của góc ABC cắt AC ở E. Kẻ EH vuông góc với BC
a) Chứng minh tam giác ABE bằng tam giác HBE
b) Chứng minh HB = HC
c) Từ H kẻ đường thẳng song song với BE cắt AC ở K. Chứng minh tam giác EHK đều
d) Gọi I là giao điểm của BA và HE. Chứng minh IE > EH
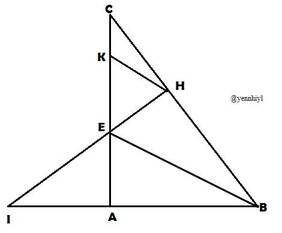
a) Xét \(\Delta ABE\) và \(\Delta HBE\):
BE chung
\(\widehat{ABE}=\widehat{EBH}\)
\(\widehat{EAB}=\widehat{EHB}=90^o\)
\(\Rightarrow\Delta ABE=\Delta HBE\left(ch-gn\right)\)
b) \(\widehat{EBH}=\dfrac{1}{2}\widehat{B}=30^o\)
\(\widehat{ACB}=90^o-\widehat{B}=30^o\)
\(\Rightarrow\Delta EBC\) cân tại E
Mà EH vuông góc BC
\(\Rightarrow HB=HC\)
c) \(\widehat{HEB}=90^o-\widehat{EBH}=60^o\)
\(KH//BE\Rightarrow\widehat{KHE}=\widehat{HEB}=60^o\)
\(\widehat{HEB}+\widehat{AEB}=60^o+60^o=120^o\)
\(\Rightarrow\widehat{KEH}=180^o-120^o=60^o\)
\(\Rightarrow\Delta EHK\) đều
d) Theo phần a. \(\Delta ABE=\Delta HBE\Rightarrow AE=EH\)
\(\Delta IAE\) vuông ở A \(\Rightarrow IE>AE\)
\(\Rightarrow IE>EH\)
Đúng 2
Bình luận (0)
a) Xét ΔABEΔABE và ΔHBEΔHBE:
BE chung
ˆABE=ˆEBHABE^=EBH^
ˆEAB=ˆEHB=90oEAB^=EHB^=90o
⇒ΔABE=ΔHBE(ch−gn)⇒ΔABE=ΔHBE(ch−gn)
b) ˆEBH=12ˆB=30oEBH^=12B^=30o
ˆACB=90o−ˆB=30oACB^=90o−B^=30o
⇒ΔEBC⇒ΔEBC cân tại E
Mà EH vuông góc BC
⇒HB=HC⇒HB=HC
c) ˆHEB=90o−ˆEBH=60oHEB^=90o−EBH^=60o
KH//BE⇒ˆKHE=ˆHEB=60oKH//BE⇒KHE^=HEB^=60o
ˆHEB+ˆAEB=60o+60o=120oHEB^+AEB^=60o+60o=120o
⇒ˆKEH=180o−120o=60o⇒KEH^=180o−120o=60o
⇒ΔEHK⇒ΔEHK đều
d) Theo phần a. ΔABE=ΔHBE⇒AE=EHΔABE=ΔHBE⇒AE=EH
ΔIAEΔIAE vuông ở A ⇒IE>AE
Đúng 0
Bình luận (0)
cho tam giác ABC có 3 góc nhọn. và AB<AC
kẻ BE vuông góc với Ac tại E, CF vuông góc với AB tại F, BE cắt CF tại H
kẻ HQ song song với AC, HP song song với AB ( Q thuộc AB, P thuộc AC)
a) cm: Tam giác AHQ=tam giác HAP
b) cho M là trung điểm của BC.
cm: tam giác MEF cân và góc AEF=góc ABC
c) cm: HA+HB+HC<2/3(AB+AC+BC)
a: Xét tứ giác AQHP có
AQ//HP
AP//HQ
=>AQHP là hình bình hành
Xet ΔAHQ và ΔHAP có
HA chung
HQ=AP
AQ=HP
=>ΔAHQ=ΔHAP
b: ΔFBC vuông tại F
mà FM là trung tuyến
nên FM=BC/2
ΔECB vuông tại E
mà EM là trung tuyến
nên EM=BC/2=FM
=>ΔMEF cân tại M
góc BFC=góc BEC=90 độ
=>BFEC nội tiếp
=>góc AEF=góc ABC
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại B , kẻ BE vuông góc với AC . tìm số đo các góc nhọn của tam giác ABC biết EC-EA=AB
Cho tam giác abc vuông tại a kẻ đường phân giác Be (e thuộc ac )Kẻ AH vuông góc với BC (H thuộc BC) Chứng minh
a, tam giác Abe bằng tam giác HEBb ,be là đường trung trực của ABc,Gọi K là giao điểm của BA và EH so sánh EKvà EHd, BE vuông góc KC
giải giùm mình nhanh với ạ mình đang cần gấp
a: Xét ΔBAE vuông tại A và ΔBHE vuông tại H có
EB chung
góc ABE=góc HBE
=>ΔBAE=ΔBHE
=>BA=BH; EA=EH
=>EB là trung trực của AH
c: EA=EH
mà EA<EK
nên EH<EK
d: Xét ΔBHK vuông tại H và ΔBAC vuông tại A có
BH=BA
góc HBK chung
=>ΔBHK=ΔBAC
=>BK=BC
=>ΔBKC cân tại B
mà BE là phân giác
nen BE vuông góc KC
Đúng 3
Bình luận (1)
bạn có thể cho mh xem hình được k
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB = AC. Kẻ BE Vuông góc với AC tại E, CF vuông góc với AV tại F, BE cắt CF tại I. Chứng minh rằng AE = AF
Lời giải:
Xét tam giác $ABE$ và $ACF$ có:
$\widehat{A}$ chung
$AB=AC$ (gt)
$\widehat{AEB}=\widehat{AFC}=90^0$
$\Rightarrow \triangle ABE=\triangle ACF$ (ch-gn)
$\Rightarrow AE=AF$
Đúng 0
Bình luận (0)






















