Cho tam giác ABC có 3 góc nhọn. Dựng ra phía ngoài 2 tam giác vuông can đỉnh A là ABD và ACE. Gọi M;N;P lần lượt là trung điểm của BC;BD;CE.
a) Chứng minh: BE = CD và BE vuoongh góc với CD
b) Chứng minh tam giác MNP vuông cân
Những câu hỏi liên quan
Cho tam giác ABC có 3 góc nhọn. Dựng ra phía ngoài 2 tam giác vuông cân đỉnh A là ABD và ACE . Gọi M;N;P lần lượt là trung điểm của BD; CE; BC .
Chứng minh tam giác MNP vuông cân
Cho tam giác ABC có góc A nhọn, phía ngoài tam giác vẽ các tam giác vuông cân tại A là ABD, ACE. Gọi M là trung điểm của BC. Cm AM 1/2 DE và AM vuông góc DECho tam giác ABC có góc A nhọn, phía ngoài tam giác vẽ các tam giác vuông cân tại A là ABD, ACE. Gọi M là trung điểm của BC. Cm AM 1/2 DE và AM vuông góc DECho tam giác ABC có góc A nhọn, phía ngoài tam giác vẽ các tam giác vuông cân tại A là ABD, ACE. Gọi M là trung điểm của BC. Cm AM 1/2 DE và AM vuông góc DE
Đọc tiếp
Cho tam giác ABC có góc A nhọn, phía ngoài tam giác vẽ các tam giác vuông cân tại A là ABD, ACE. Gọi M là trung điểm của BC. Cm AM = 1/2 DE và AM vuông góc DECho tam giác ABC có góc A nhọn, phía ngoài tam giác vẽ các tam giác vuông cân tại A là ABD, ACE. Gọi M là trung điểm của BC. Cm AM = 1/2 DE và AM vuông góc DECho tam giác ABC có góc A nhọn, phía ngoài tam giác vẽ các tam giác vuông cân tại A là ABD, ACE. Gọi M là trung điểm của BC. Cm AM = 1/2 DE và AM vuông góc DE
Cho tam giác nhọn ABC. Về phía ngoài tam giác ABC vẽ các tam giác ABD vuông cân đỉnh B, tam giác ACE vuông cân đỉnh C. Gọi M là giao điểm của BE và CD. C/m rằng : AM vuông góc BC.
cho tam giác ABC nhọn. vẽ ra phía ngoài tam giác ABC hai tam giác vuông cân là ABD và ACE. gọi M là trung điểm BC. CMR: a,2AM=DE b,AM vuông góc DE
cho tam giác ABC nhọn. vẽ ra phía ngoài tam giác ABC hai tam giác vuông cân là ABD và ACE. gọi M là trung điểm BC. CMR: a,2AM=DE b,AM vuông góc DE
cho tam giác ABC nhọn. vẽ ra phía ngoài tam giác ABC hai tam giác vuông cân là ABD và ACE. gọi M là trung điểm BC. CMR: góc DME vuông
Dựng ra phía ngoài tam giác vuông cân ABC đỉnh A các tam giác đều ABD và ACE. Góc giữa hai đường thẳng BE và CD là: A.
90
o
B.
60
o
C.
45
o
D.
30
o
Đọc tiếp
Dựng ra phía ngoài tam giác vuông cân ABC đỉnh A các tam giác đều ABD và ACE. Góc giữa hai đường thẳng BE và CD là:
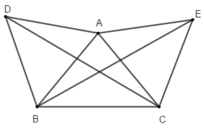
A. 90 o
B. 60 o
C. 45 o
D. 30 o
Xét phép quay tâm A góc quay 60 o biến D thành B và biến C thành E, suy ra phép quay đó biến đường thẳng DC thành đường thẳng BE suy ra góc giữa DC và BE bằng góc quay 60 o .
Chọn đáp án B.
Đúng 0
Bình luận (0)
Cho tam giác ABC có góc A nhọn. Vẽ bên ngoài các tam giác vuông cân đỉnh A là tam giác ABD và tam giác ACE. Gọi M là trung điểm BC. Chứng minh: AM vuông góc với BD.
AM vuông góc với DE chứ.
\(\overrightarrow{AM}=\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right);\overrightarrow{DE}=\left(\overrightarrow{AE}-\overrightarrow{AD}\right)\)
\(\Rightarrow\overrightarrow{AM}.\overrightarrow{DE}=\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\left(\overrightarrow{AE}-\overrightarrow{AD}\right)\)
\(=\dfrac{1}{2}\left(\overrightarrow{AB}.\overrightarrow{AE}-\overrightarrow{AC}.\overrightarrow{AD}-\overrightarrow{AB}.\overrightarrow{AD}+\overrightarrow{AC}.\overrightarrow{AE}\right)\)
\(=\dfrac{1}{2}\left[AB.AE.cos\left(\widehat{BAC}+90^o\right)-AC.AD.cos\left(\widehat{BAC}+90^o\right)-AB.AD.cos90^o+AC.AE.cos90^o\right]\)
\(=0\)
\(\Rightarrow AM\perp DE\)
Đúng 0
Bình luận (1)
Cách giải lớp 8 (khá loằng ngoằng):
Vẽ hbh AEID , AJED
Gọi O là trung điểm IA
Ta có: góc BAC = góc IAD (cùng bù góc DAE)
Xét tam giác ADI và ABC có:
góc BAC = góc IAD (cmt)
AB = AD (gt)
AC = DI (do cùng bằng AE)
=> 2 tam giác bằng nhau (c-g-c)
=> BC = IA và góc ACM = góc AID
=> MC = OA (vì BC = 2MC và IA = 2OA)
Xét tam giác AMC và AOE có:
AC = AE (gt)
MC = OA (cmt)
góc ACM = góc OAE ( cùng bằng góc AID)
=> 2 tam giác bằng nhau (c-g-c)
=> góc MAC = góc OEA
Mà góc OEA = góc EAJ (sole tr vì DE // AJ)
=> góc MAC = góc EAJ
Ta có :góc EAJ + góc JAC = 90°
=> góc MAC + góc JAC = 90°
Hay góc MAJ = 90°
=> AM vuông góc AJ
Mà AJ // DE
=> AM vuông góc DE (đpcm)
Đúng 0
Bình luận (0)
Dựng ra phía ngoài tam giác vuông cân ABC đỉnh các tam giác đều ABD và ACE . Góc giữa hai đường thẳng BE và CD là: A.
90
°
B.
60
°
C.
45
°
D.
30
°
Đọc tiếp
Dựng ra phía ngoài tam giác vuông cân ABC đỉnh các tam giác đều ABD và ACE . Góc giữa hai đường thẳng BE và CD là:
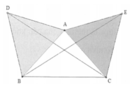
A. 90 °
B. 60 °
C. 45 °
D. 30 °
Đáp án B
Xét phép quay tâm A góc quay 60 ° biến D thành B và biến C thành E, suy ra phép quay đó biến đường thẳng CD thành đường thẳng BE suy ra góc giữa BE và CD bằng góc quay 60 °
Đúng 0
Bình luận (0)