Cho tam giác ABC vuông tại A, AB=5cm; BC=13cm.Kẻ AH vuông góc với BC tại H.Tính độ dài của đoạn thẳng AC;AH;BH;CH
(giúp em nhanh nha em cảm ơn:3)

Những câu hỏi liên quan
a)Cho tam giác ABC vuông tại A, biết AB=4cm; BC=5cm, Tonhs cosC+TanB
b) Cho tam giác ABC vuông tại A, có AB=5cm,BC=10cm. Tính sinC và số đo góc B
c) Cho tam giác ABC vuông tại A, biết cosB=8cm. hãy tính các tỉ số lượng giác của góc C. E c.ơn ạ!
Câu a) với b) tính cos, tan, sin là tính góc hay cạnh vậy cậu?
Đúng 0
Bình luận (9)
a) Xét \(\Delta ABC\) vuông tại `A`
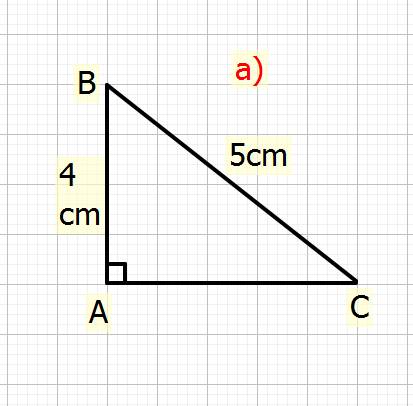
Ta có: \(BC^2=AB^2+AC^2\) (đl Pytago)
\(\Rightarrow5^2=4^2+AC^2\\ \Rightarrow AC^2=5^2-4^2\\ \Rightarrow AC^2=25-16=9\\ \Rightarrow AC=\sqrt{9}=3cm\)
Vậy: \(AC=3cm\)
Ta có: \(CosC=\dfrac{AC}{BC}\left(tslg\right)\)
\(\Rightarrow CosC=\dfrac{3}{5}\\ \Rightarrow CosC\approx53^o\)
Vậy: Góc C khoảng \(53^o\)
Ta có: \(TanB=\dfrac{AC}{AB}\left(tslg\right)\)
\(\Rightarrow TanB=\dfrac{3}{4}\\ \Rightarrow TanB\approx37^o\)
Vậy: Góc B khoảng \(37^o\)
_
b) Xét \(\Delta ABC\) vuông tại `A`
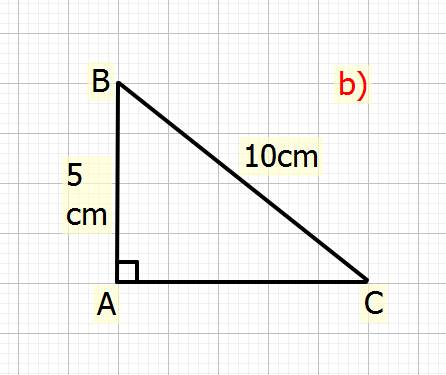
Ta có: \(BC^2=AB^2+AC^2\) (đl Pytago)
\(\Rightarrow10^2=5^2+AC^2\\ \Rightarrow AC^2=10^2-5^2\\\Rightarrow AC^2=100-25=75\\ \Rightarrow AC=\sqrt{75}=5\sqrt{3}cm\)
Vậy: \(AC=5\sqrt{3}cm\)
Ta có: \(SinC=\dfrac{AB}{BC}\left(tslg\right)\)
\(\Rightarrow SinC=\dfrac{5}{10}\\ \Rightarrow30^o\)
Vậy: Góc C là \(30^o\)
Ta có: \(SinB=\dfrac{AC}{BC}\left(tslg\right)\)
\(\Rightarrow SinB=\dfrac{5\sqrt{3}}{10}\\ \Rightarrow SinB=60^o\)
Vậy: Góc B là \(60^o\).
Đúng 1
Bình luận (2)
Cho tam giác ABC vuông tại A có AB\(=\) 3cm, BC \(=5cm.\)
Tính diện tích tam giác ABC
Áp dụng định lí Pytago có:
\(AC=\sqrt{BC^2-AB^2}=\sqrt{5^2-3^2}=4\left(cm\right)\)
\(\Rightarrow S_{ABC}=\dfrac{AB.AC}{2}=\dfrac{3.4}{2}=6\left(cm^2\right)\)
Đúng 2
Bình luận (2)
Diện tích tam giác ABC là:
( 3. 5 ): 2 = 7.5 ( cm2)
Đ/s:...
Đúng 1
Bình luận (3)
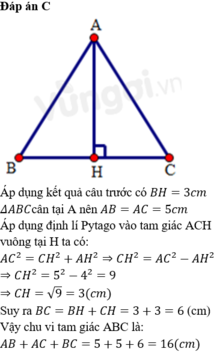
Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC tại H. Cho AH=4cm,AB=5cm
Chu vi tam giác ABC
A. 18 (cm)
B. 15 (cm)
C. 16 (cm)
D. 20 (cm)
cho tam giác ABC có BC = 12cm , AC = 5cm , AB = 13cm . Chọn khẳng định đúng
A . tam giác ABC là tam giác vuông tại A
B. tám giác ABC là tam giác nhọn
C. tam giác ABC là tam giác vuông tại C
D . tam giác ABC là tam giác tù
Xem thêm câu trả lời
Cho tam giác ABC vuông tại A. Tính BC biết :
a) AB= √8cm, AC= √17cm
b) AB= 3/5cm, AC= 4/5cm
Xét tg ABC vuông tại A, có:
a. \(BC^2=AB^2+AC^2\left(Pytago\right)\)
\(=>BC=\sqrt{AB^2+AC^2}=\sqrt{\left(\sqrt{8}\right)^2+\left(\sqrt{17}\right)^2}=5\left(cm\right)\)
b. \(BC^2=AB^2+AC^2\left(Pytago\right)\)
\(=>BC=\sqrt{AB^2+AC^2}=\sqrt{\left(\dfrac{3}{5}\right)^2+\left(\dfrac{4}{5}\right)^2}=1\left(cm\right)\)
Đúng 2
Bình luận (0)
a, Xét Tam giác ABC vuôgn tại A
Theo định lí Pi-ta-go, ta có:
\(AB^2+AC^2=BC^2\)
Hay \(\sqrt{8}+\sqrt{17}=\sqrt{25}=5\left(cm\right)\)
Vậy BC = 5 (cm)
b, Xét tam giác ABC vuôgn tại A
THeo định lí Pi-ta-go, ta có :
\(AB^2+AC^2=BC^2\)
hay \(\left(\dfrac{3}{5}\right)^2+\left(\dfrac{4}{5}\right)^2=\sqrt{\dfrac{9}{25}+\dfrac{16}{25}=1}\)
Vậy BC = 1cm
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A có BC = 5cm, AB = 4cm, tính diện tích tam giác ABC là bao nhiêu?
đ/l pytago:
AC^2=BC^2-AB^2
=>AC=3cm
SABC=\(\dfrac{AB.AC}{2}=6cm^2\)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A, biết AB = 3 cm, BC = 5cm. Tính diện tích tam giác ABC
Xét \(\Delta ABC\)vuông tại A
=>AB2 +AC2=BC2
32+AC2=52=> AC2=52-32= 25-9=16
=> AC=\(\sqrt{16}\)=4
Diện tích \(\Delta ABC\) là: (ACxAB)/2=4x3/2=12/2=6(cm2)
Vậy: diện tích am giác ABC là 6 cm2
Đúng 1
Bình luận (0)
bạn dùng định lí pitago để tính cạnh AC nhé. AC=căn 34. sau khi có 3 cạnh thì tính diện tích
Đúng 0
Bình luận (0)
Áp dụng định lí Py ta go vào tam giác ABC có:
AC2= BC2-AB2=52-32=25-9=16(cm)
=>AC=4(cm)
Diện tích tam giác ABC là:
3.4:2=6(cm)
ĐS:6cm
Chúc bn học giỏi nhoa ~
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC vuông tại A, đường cao AH. Vẽ HE vuông góc với AB tại E, HF vuông góc với AC tại F a, giải tam giác ABC biết AB = 5cm, AC =12cm b, CM: tam giác AEF đồng dạng tam giác ACB c, CM: BE = BCsin^3C
Bài 1 Cho tam giác ABC vuông tại A có đường cao AH cho AB5cm,BH3cma)Tính BC,AHb) Kẻ HE vuông góc vs AC .Tính HEBài 2Cho tam giác ABC vuông tại A đường cao AH phân giác AD biết BD10cm,DC20cm.Tính AH,HDBaif3a) cho tam giác ABC vuông tại A có AB5cm đg cao AH4cm. Tính chu vi tam giác ABCb) cho tam giác ABC vuông tại A đg cao AH phân giác AD.biết BD 15cm DC20cm Tính AH,ADGiải nhanh giúp mk nha mk c.ơn
Đọc tiếp
Bài 1
Cho tam giác ABC vuông tại A có đường cao AH cho AB=5cm,BH=3cm
a)Tính BC,AH
b) Kẻ HE vuông góc vs AC .Tính HE
Bài 2
Cho tam giác ABC vuông tại A đường cao AH phân giác AD biết BD=10cm,DC=20cm.Tính AH,HD
Baif3
a) cho tam giác ABC vuông tại A có AB=5cm đg cao AH=4cm. Tính chu vi tam giác ABC
b) cho tam giác ABC vuông tại A đg cao AH phân giác AD.biết BD =15cm DC=20cm Tính AH,AD
Giải nhanh giúp mk nha mk c.ơn
BÀI 1:
a)
· Trong ∆ ABC, có: AB2= BC.BH
Hay BC= ![]() =
= ![]()
· Xét ∆ ABC vuông tại A, có:
AB2= BH2+AH2
↔AH2= AB2 – BH2
↔AH= ![]() =4 (cm)
=4 (cm)
b)
· Ta có: HC=BC-BH
àHC= 8.3 - 3= 5.3 (cm)
· Trong ∆ AHC, có:

· ![]()
Đúng 0
Bình luận (0)
Bài 1:
a) Áp dụng hệ thức lượng ta có:
\(AB^2=BH.BC\)
\(\Rightarrow\)\(BC=\frac{AB^2}{BH}\)
\(\Rightarrow\)\(BC=\frac{5^2}{3}=\frac{25}{3}\)
Áp dụng Pytago ta có:
\(AH^2+BH^2=AB^2\)
\(\Rightarrow\)\(AH^2=AB^2-BH^2\)
\(\Rightarrow\)\(AH^2=5^2-3^2=16\)
\(\Rightarrow\)\(AH=4\)
b) \(HC=BC-BH=\frac{25}{3}-3=\frac{16}{3}\)
Áp dụng hệ thức lượng ta có:
\(\frac{1}{HE^2}=\frac{1}{AH^2}+\frac{1}{HC^2}\)
\(\Leftrightarrow\)\(\frac{1}{HE^2}=\frac{1}{4^2}+\frac{1}{\left(\frac{16}{3}\right)^2}=\frac{25}{256}\)
\(\Rightarrow\)\(\frac{1}{HE}=\frac{5}{16}\)
\(\Rightarrow\)\(HE=\frac{16}{5}\)
Đúng 0
Bình luận (0)
Bài 1: Cho tam giác ABC vuông tại A, đường cao AH = 5cm. Biết CH = 6cm. tính:
a) AB, AC,BC và BH?
b) Diện tích tam giác ABC
Bài2: Cho tam giác ABC vuông tại A, đường cao AH; AB = 15cm; BC = 25cm. BTính:
a) AC,AH, HC và BH?
b) Diện tích tam giác ABC
\(1,\)
\(a,\) Áp dụng HTL tam giác
\(\left\{{}\begin{matrix}AH^2=CH\cdot BH\\AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}BH=\dfrac{AH^2}{CH}=\dfrac{25}{6}\left(cm\right)\\AB=\sqrt{\dfrac{25}{6}\left(\dfrac{25}{6}+6\right)}=\dfrac{5\sqrt{61}}{6}\left(cm\right)\\AC=\sqrt{6\left(\dfrac{25}{6}+6\right)}=\sqrt{61}\left(cm\right)\end{matrix}\right.\\ BC=\dfrac{25}{6}+6=\dfrac{61}{6}\left(cm\right)\)
\(b,S_{ABC}=\dfrac{1}{2}AH\cdot BC=\dfrac{1}{2}\cdot5\cdot\dfrac{61}{6}=\dfrac{305}{12}\left(cm^2\right)\)
Đúng 3
Bình luận (0)