\(1,HC=\dfrac{AH^2}{BH}=\dfrac{256}{9}\\ \Rightarrow AB=\sqrt{BH\cdot BC}=\sqrt{\left(\dfrac{256}{9}+9\right)9}=\sqrt{337}\\ 2,BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\\ \Rightarrow BH=\dfrac{AB^2}{BC}=6,4\left(cm\right)\\ 3,AC=\sqrt{BC^2-AB^2}=9\\ \Rightarrow CH=\dfrac{AC^2}{BC}=5,4\\ 4,AC=\sqrt{BC\cdot CH}=\sqrt{9\left(6+9\right)}=3\sqrt{15}\\ 5,AC=\sqrt{BC^2-AB^2}=4\sqrt{7}\left(cm\right)\\ \Rightarrow AH=\dfrac{AB\cdot AC}{BC}=3\sqrt{7}\left(cm\right)\\ 6,AC=\sqrt{BC\cdot CH}=\sqrt{12\left(12+8\right)}=4\sqrt{15}\left(cm\right)\)

Bài 1: (bạn tự vẽ hình vì hình cũng dễ)

Ta có: AB = AH + BH = 1 + 4 = 5 (cm)

Vì tam giác ABC cân tại B => BA = BC => BC = 5 (cm)

Xét tam giác BCH vuông tại H có:

  \(HB^2+CH^2=BC^2\left(pytago\right)\)

  \(4^2+CH^2=5^2\)

  \(16+CH^2=25\)

\(\Rightarrow CH^2=25-16=9\)

\(\Rightarrow CH=\sqrt{9}=3\left(cm\right)\)

Tới đây xét tiếp pytago với tam giác ACH là ra AC nhé

Bài 2: Sử dụng pytago với tam giác ABH => AH

Sử dụng pytago với ACH => AC

bạn cần bài nào

2 BÀI CHẢ BT HỎI BÀI NÀO

Cần bài nào hả bn

Bài 2: 

a: \(BC=\sqrt{8^2+6^2}=10\left(cm\right)\)

b: \(BC=\sqrt{12^2+16^2}=20\left(cm\right)\)

c: \(BC=\sqrt{5^2+12^2}=13\left(cm\right)\)

Bài 1:

a: ΔABC vuông tại A

=>\(BC^2=AB^2+AC^2\)

=>\(BC^2=6^2+8^2=100\)

=>BC=10(cm)

Xét ΔABC vuông tại A có \(sinC=\dfrac{AB}{BC}=\dfrac{3}{5}\)

nên \(\widehat{C}\simeq37^0\)

=>\(\widehat{B}=90^0-37^0=53^0\)

b: Xét ΔHAB vuông tại H có HG là đường cao

nên \(AG\cdot AB=AH^2\left(1\right)\)

Xét ΔAHC vuông tại H có HK là đường cao

nên \(AK\cdot AC=AH^2\left(2\right)\)

Từ (1) và (2) suy ra \(AG\cdot AB=AK\cdot AC\)

Câu a) với b) tính cos, tan, sin là tính góc hay cạnh vậy cậu?

a) Xét \(\Delta ABC\) vuông tại `A`

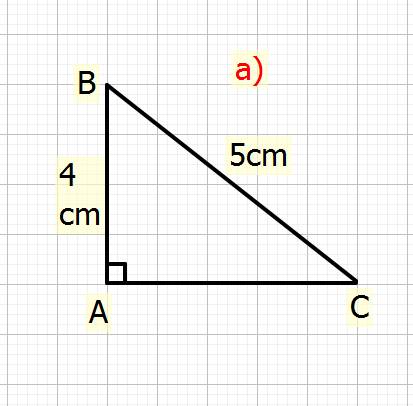
Ta có: \(BC^2=AB^2+AC^2\) (đl Pytago)

\(\Rightarrow5^2=4^2+AC^2\\ \Rightarrow AC^2=5^2-4^2\\ \Rightarrow AC^2=25-16=9\\ \Rightarrow AC=\sqrt{9}=3cm\) 

Vậy: \(AC=3cm\)

Ta có: \(CosC=\dfrac{AC}{BC}\left(tslg\right)\)

\(\Rightarrow CosC=\dfrac{3}{5}\\ \Rightarrow CosC\approx53^o\)

Vậy: Góc C khoảng \(53^o\)

Ta có: \(TanB=\dfrac{AC}{AB}\left(tslg\right)\)

\(\Rightarrow TanB=\dfrac{3}{4}\\ \Rightarrow TanB\approx37^o\)

Vậy: Góc B khoảng \(37^o\) 

_

b) Xét \(\Delta ABC\) vuông tại `A`

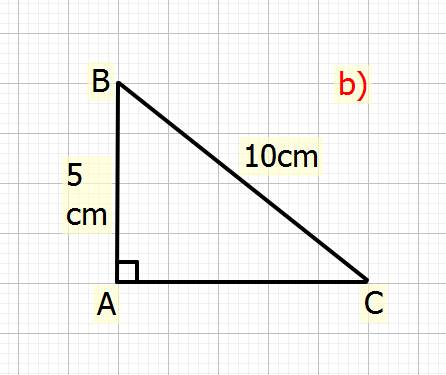
Ta có: \(BC^2=AB^2+AC^2\) (đl Pytago)

\(\Rightarrow10^2=5^2+AC^2\\ \Rightarrow AC^2=10^2-5^2\\\Rightarrow AC^2=100-25=75\\ \Rightarrow AC=\sqrt{75}=5\sqrt{3}cm\)

Vậy: \(AC=5\sqrt{3}cm\)

Ta có: \(SinC=\dfrac{AB}{BC}\left(tslg\right)\)

 \(\Rightarrow SinC=\dfrac{5}{10}\\ \Rightarrow30^o\)

Vậy: Góc C là \(30^o\)

Ta có: \(SinB=\dfrac{AC}{BC}\left(tslg\right)\)

\(\Rightarrow SinB=\dfrac{5\sqrt{3}}{10}\\ \Rightarrow SinB=60^o\)

Vậy: Góc B là \(60^o\).