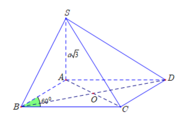
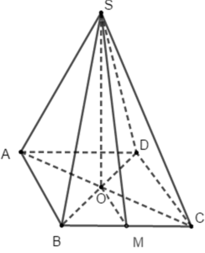
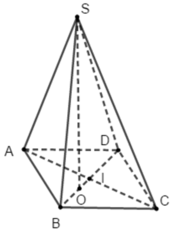
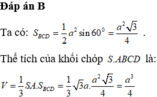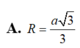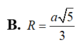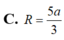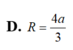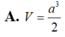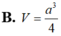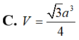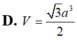Cho hình chóp S.ABCD có đáy ABCD là hình thoi với cạnh a 3 ; B A D ^ = 120 o và cạnh bên SA ⊥ (ABCD). Biết số đo của góc giữa hai mặt phẳng ( SBC ) và ( ABCD ) bằng 60 o . Tính khoảng cách d giữa hai đường thẳng BD và SC.
A. d = a 29 26
B. d = 3 a 29 26
C. d = 3 a 39 13
D. d = a 16 6