Bài 1:Tính chu vi tam giác biết:
a)AB=4cm;AC=7cm
b)AB=11cm;AC=5cm
Những câu hỏi liên quan
Bài 1: Cho tam giác vuông ABC, vuông góc tại A. Chu vi tam giác là 75cm, Cạnh BC là 45cm. Hỏi:a) Tổng độ dài của cạnh AB và AC là bao nhiêu?b) Tính diện tích tam giác vuông ABC, biết cạnh AB hơn cạnh AC là 4cm. Bài 2: Cho tam giác ABC có chu vi 67cm, cạnh AB và AC có tổng độ dài 47 cm.a) Tính độ dài BC.b) Tính diện tích tam giác ABC, biết chiều cao AH là 15cm. Bài 3: Một tam giác vuông có cạnh góc vuông thứ nhất là 24cm, cạnh góc vuông thứ hai bằng 5/8 cạnh góc vuông thứ nhất. Tính di...
Đọc tiếp
Bài 1: Cho tam giác vuông ABC, vuông góc tại A. Chu vi tam giác là 75cm, Cạnh BC là 45cm. Hỏi:
a) Tổng độ dài của cạnh AB và AC là bao nhiêu?
b) Tính diện tích tam giác vuông ABC, biết cạnh AB hơn cạnh AC là 4cm.
Bài 2: Cho tam giác ABC có chu vi 67cm, cạnh AB và AC có tổng độ dài 47 cm.
a) Tính độ dài BC.
b) Tính diện tích tam giác ABC, biết chiều cao AH là 15cm.
Bài 3: Một tam giác vuông có cạnh góc vuông thứ nhất là 24cm, cạnh góc vuông thứ hai bằng 5/8 cạnh góc vuông thứ nhất. Tính diện tích tam giác vuông đó.
Bài 4: Cho tam giác vuông ABC, vuông góc tại A. Chu vi tam giác là 90cm, Cạnh BC là 45cm. Hỏi:
a) Tổng độ dài của cạnh AB và AC là bao nhiêu?
b)Tính diện tích tam giác vuông ABC, biết cạnh AC bằng 4/5 cạnh AB.
Bài 1:
a: AB+AC=75-45=30(cm)
b: AB=(30+4):2=17(cm)
=>AC=13cm
\(S=17\cdot13=221\left(cm^2\right)\)
Bài 2:
a: BC=67-47=20(cm)
b: \(S=\dfrac{15\cdot20}{2}=15\cdot10=150\left(cm^2\right)\)
Đúng 0
Bình luận (1)
Bài 1:Tính chu vi tam giác biết:
a)AB=4cm;AC=7cm
b)AB=11cm;AC=5cm
13 tháng 2 2022 lúc 14:26
Bài 19: Cho tam giác ABC có chu vi 18cm, các đường phân giác BD và CE. Tính các cạnh của tam giác ABC, biết A. AC 4cm, BC 8cm, AB 6cmB. AB 4cm, BC 6cm, AC 8cmC. AB 4cm, BC 8cm, AC 6cmD. AB 8cm, BC 4cm, AC 6cm
Đọc tiếp
Bài 19: Cho tam giác ABC có chu vi 18cm, các đường phân giác BD và CE. Tính các cạnh của tam giác ABC, biết 
A. AC = 4cm, BC = 8cm, AB = 6cm
B. AB = 4cm, BC = 6cm, AC = 8cm
C. AB = 4cm, BC = 8cm, AC = 6cm
D. AB = 8cm, BC = 4cm, AC = 6cm
TK
Vậy AB = 4cm, BC = 8cm, AC = 6cm
Đáp án cần chọn là: C
Đúng 5
Bình luận (0)
Bài 4:Cho tam giác ABC vuông tại B, biết AB = 4cm, BC = 6cm.
a) Tính AC, chu vi tam giác ABC
a: \(AC=\sqrt{AB^2+BC^2}=2\sqrt{13}\left(cm\right)\)
\(C=AB+BC+AC=10+2\sqrt{13}\left(cm\right)\)
Đúng 2
Bình luận (1)
Áp dụng định lí Py - ta - go vào tam giác vuông ABC ta có:
\(AC=\sqrt{4^2+6^2}=\sqrt{52}=2\sqrt{13}\)
Chu vi tam giác ABC là:
\(4+6+2\sqrt{13}=10+2\sqrt{13}\)
Đúng 1
Bình luận (0)
Bài 1: Cho tam giác ABC cân có AB=4cm;BC=9cm
a)Tính độ dài AC
b)Tính chu vi tam giác ABC
a)
ta có t/g ABC cân tại A
->AB=AC=4Cm(đ nghĩa của t/g cân)
b)
chu vi của t/g ABC:
AB +AC+BC
->(4 X 2)+9
->17cm
Vậy chu vi của tam giác ABC là 17cm
(KO CHẮC LÀ ĐÚNG NHA)
HI HI ^ _^
Đúng 0
Bình luận (0)
giải sai rồi
học bất đẳng thức tam giác chưa AB+AC>BC
cạnh BC - AB< AC<BC + AB
<=>9-4<AC<9+4
<=>5<AC<13
=>AC=9 cm
chu vi tam giác là 9+9+4 =22cm
Đúng 0
Bình luận (0)
Bài 1: Cho Tam giác ABC = Tam giác DEF. BIết góc A=27 độ, góc F=52 độ. Tính các góc còn lại của tam giác?
Bài 2:Cho Tam giác ABC = Tam giác MNP. Biết AB+BC=7cm, MN-NP=3cm, MP=4cm. Tính chu vi của mỗi tam giác?
Bài 3: Cho Tam giác ABC = Tam giác POR. Biết góc Q=55 độ, 3.góc A=2. góc C. Tính các góc còn lại của mỗi tam giác trên?
bài 1 theo bài ra có tam giác abc=def
a=27do f=52do
mà a=d
=>a=d=27do
=> d=27 do
f=c=52do
=>c =52do
goc b=e
ma ta co a+b+c=d+e+f=180do
thay số 27+b+52=27+e+52=180
=>b=180-(27+52)=101
=>b=e=101
Đúng 1
Bình luận (0)
Cho 2 tam giác ABC và MNP đồng dạng với nhau. Biết chu vi tam giác ABC là 40cm; AB = 4cm; MN = 10cm . Tính chu vi tam giác MNP?
A. 50cm
B. 60cm
C. 100cm
D. 80cm
Vì tam giác ABC đồng dạng với tam giác MNP nên;
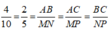
Theo tính chất dãy tỉ số bằng nhau ta có:
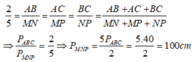
Chọn đáp án C
Đúng 0
Bình luận (0)
1. Cho tam giác ABC = tam giác MNP . Biết AB = 4cm, AC = 6cm , NP = 7cm . Tính chu vi của tam giác MNP.
Ta thấy cạnh NP tương ứng với cạnh CB của tam giác ABC
=> Chu vi tam giác ABC là :
4+6+7 = 17 ( cm)
=> Chu vi tam giác MNP là 17 cm
Vậy chu vi tam giác MNP là 17 cm
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH. Biết AB 3cm, AC 4cm. Tính độ dài đường cao AH, tính
c
o
s
A
C
B
^
và chu vi tam giác ABH. A. AH 2,8 cm;
c
o
s
A
C
B
^
3
5
B. AH 2,4 cm; ...
Đọc tiếp
Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 3cm, AC = 4cm. Tính độ dài đường cao AH, tính c o s A C B ^ và chu vi tam giác ABH.
A. AH = 2,8 cm; c o s A C B ^ = 3 5
B. AH = 2,4 cm; c o s A C B ^ = 4 5
C. AH = 2,5 cm; c o s A C B ^ = 3 4
D. AH = 1,8 cm; c o s A C B ^ = 2 3
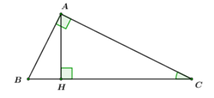
Áp dụng định lý Pytago trong ∆ ABC vuông tại A ta có:
Áp dụng hệ thức lượng trong ∆ ABC vuông tại A có đường cao AH ta có:
Đáp án cần chọn là: B
Đúng 2
Bình luận (0)
Cho ΔABC = ΔDEF. Tính chu vi mỗi tam giác nói trên biết rằng AB = 4cm, BC = 6cm, DF = 5cm (chu vi mỗi tam giác là tổng độ dài ba cạnh của tam giác đó).
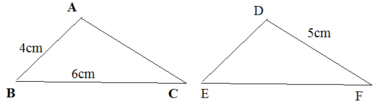
Vì ΔABC = ΔDEF nên suy ra:
AB = DE = 4cm
BC = EF = 6cm
DF = AC = 5cm
Chu vi tam giác ABC bằng:
AB + BC + CA = 4 + 6 + 5 = 15 (cm)
Chu vi tam giác DEF bằng:
DE + EF + DF = 4 + 6 + 5 = 15 (cm)
Đúng 0
Bình luận (0)