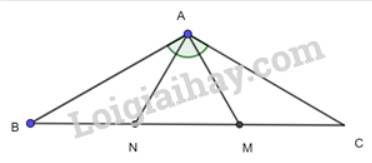
a) Xét 2 tam giác vuông BAM và CAN có:

\(\widehat{BAM} = \widehat{CAM}(=90^0)\)

AB=AC (Do tam giác ABC cân tại A)

\(\widehat B = \widehat C\) (Do tam giác ABC cân tại A)

=>\(\Delta BAM = \Delta CAN\)(g.c.g)

b) Cách 1: 

Xét tam giác ABC cân tại A, có \(\widehat {A{\rm{ }}} = 120^\circ \) có:

\(\widehat B = \widehat C = \frac{{{{180}^o} - {{120}^o}}}{2} = {30^o}\).

Xét tam giác ABM vuông tại A có:

\(\widehat {B} + \widehat {BAM} + \widehat {AMB} = {180^o}\\ \Rightarrow {30^o} + {90^o} + \widehat {AMB} = {180^o}\\ \Rightarrow \widehat {AMB} = {60^o}\\ \Rightarrow \widehat {AMC} = {180^o} - \widehat {AMB} = {180^o} - {60^o} = {120^o}\)

Xét tam giác MAC có:

\(\begin{array}{l}\widehat {AMC} + \widehat {MAC} + \widehat C = {180^o}\\ \Rightarrow {120^o} + \widehat {MAC} + {30^o} = {180^o}\\ \Rightarrow \widehat {MAC} = {30^o} = \widehat C\end{array}\)

\(\Rightarrow \) Tam giác AMC cân tại M.

Vì \(\Delta BAM = \Delta CAN\)

=> BM=CN ( 2 cạnh tương ứng)

=> BM+MN=CN+NM

=> BN=CM

Xét 2 tam giác ANB và AMC có:

AB=AC (cmt)

\(AN = AM\)(do \(\Delta BAM = \Delta CAN\))

BN=MC (cmt)

=>\(\Delta ANB = \Delta AMC\)(c.c.c)

Mà tam giác AMC cân tại M.

=> Tam giác ANB cân tại N.

Cách 2: 

Xét tam giác ABC cân tại A, có \(\widehat {A{\rm{ }}} = 120^\circ \) có:

\(\widehat B = \widehat C = \frac{{{{180}^o} - {{120}^o}}}{2} = {30^o}\).

Xét tam giác ABM vuông tại A có:

\(\widehat B + \widehat {BAM} + \widehat {AMB} = {180^o}\\ \Rightarrow {30^o} + {90^o} + \widehat {AMB} = {180^o}\\ \Rightarrow \widehat {AMB} = {60^o}\)

Vì \(\Delta BAM = \Delta CAN\) nên AM = AN (2 cạnh tương ứng)

=> \(\Delta AMN\) đều (Tam giác cân có 1 góc bằng 60 độ)

=> \(\widehat {NAM}=60^0\)

Ta có: \(\widehat{BAN}+\widehat{NAM}=\widehat{BAM}\)

=> \(\widehat{BAN} + 60^0=90^0\)

=> \(\widehat{BAN}=30^0\)

Xét tam giác ABN có \(\widehat{BAN}=\widehat{ABN}(=30^0\) nên \(\Delta ABN\) cân tại N.

Ta có: \(\widehat{CAM}+\widehat{NAM}=\widehat{CAN}\)

=> \(\widehat{CAM} + 60^0=90^0\)

=> \(\widehat{CAM}=30^0\)

Xét tam giác ACM có \(\widehat{CAM}=\widehat{ACM}(=30^0\) nên \(\Delta ACM\) cân tại M.

a, ta có BN VÀ CN THEO THỨ TỰ  PHÂN GIÁC CỦA GÓC B VÀ GÓC C (GT)

  NEN B1=B2=1/2B VÀ C1=C2=1/2 C MÀ GÓC B = GÓC C 

(2 GÓC Ở ĐÁY CỦA TAM GIÁC CÂN ABC) =>GÓC B2 =GỐC C2

XÉT TAM GIÁC ABD VÀ TAM GIÁC ACE CO

                              GÓC A CHUNG (GT)

                               GÓC B2 = GÓC C2

                               CANH AB=AC(GT

                         VẬY TAM GIÁC ABE=TAM GIÁC ACE (GCG) =>AD=AE

                 => TAM GIÁC AMN CÂN TẠI A

không có biết luôn á

a) Xét ΔABH vuông tại H & ΔACH vuông tại H có:

- AB = AC (vì ΔABC cân tại A)

- AH là cạnh chung

Suy ra ΔABH = ΔACH (cạnh huyền - cạnh góc vuông)

Từ đó BH = CH (hai cạnh tương ứng)

b) Từ ΔABH = ΔACH (chứng minh trên) suy ra BM = CN (hai cạnh tương ứng)

Mà AB = AC (chứng minh trên)

Suy ra AM = AB - BM = AN = AC - CN

Trong ΔAMN có AM = AN (chứng minh trên) nên ΔAMN cân tại A

c) (Sửa đề: Chứng minh ba điểm A; H; I thẳng hàng)

Xét \(\Delta AMB\) và \(\Delta AMC\).có:

AB = AC ( do tam giác ABC cân tại A )

MB = MC ( do M là trung điểm BC )

AM là cạnh chung

=>\(\Delta AMB\) =\(\Delta AMC\) (c.c.c)

=>\(\widehat {ABC}\)=\(\widehat {ACB}\)( 2 góc tương ứng)