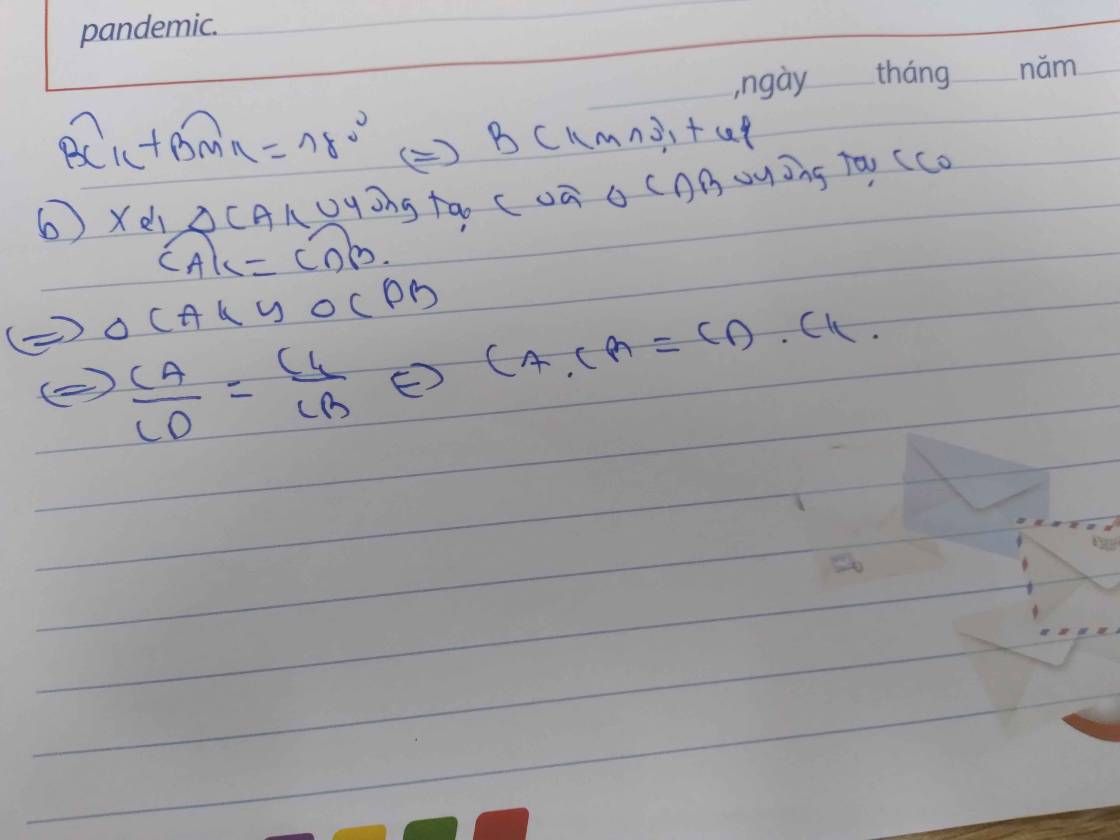Cho nửa đường tròn tâm O đường kính AB. Điểm C nằm trên O;A. (I) tiếp xúc với nửa đường tròn (O)và tiếp xúc với các đoạn thẳng CA, CD. Gọi E là tiếp điểm của AC với (I). Chứng minh: BD=BE

Những câu hỏi liên quan
Cho nửa đường tròn tâm O, đường kính AB. Lấy OA làm đường kính, vẽ nửa đường tròn nằm trên nửa mặt phẳng bờ AB chứa nửa đường tròn tâm O. Trên nửa đường tròn đường kính OA lấy điểm C không trùng với A và O, tia OC cắt nửa đường tròn tâm O tại D. Vẽ DH vuông góc với AB. CHứng minh AHCD là hình thang cân
Cho 3 điểm A;B;C theo thứ tự nằm trên 1 đường thẳng .Trên cùng 1 nửa mặt phẳng bờ AC,dựng nửa đường tròn tâm O đường kính AB ;dựng nửa đường tròn tâm O đường kính BC .Dựng tiếp tuyến chung ngoài EF(E là tiếp điểm của đường tròn tâm O;F là tiếp điểm của đường tròn tâm O).Đường thẳng AE cắt CF ở M .1)CM tứ giác BEFM nội tiếp2)CM tứ giác BEFM là hình chữ nhật
Đọc tiếp
Cho 3 điểm A;B;C theo thứ tự nằm trên 1 đường thẳng .Trên cùng 1 nửa mặt phẳng bờ AC,dựng nửa đường tròn tâm O đường kính AB ;dựng nửa đường tròn tâm O' đường kính BC .Dựng tiếp tuyến chung ngoài EF(E là tiếp điểm của đường tròn tâm O;F là tiếp điểm của đường tròn tâm O').Đường thẳng AE cắt CF ở M .
1)CM tứ giác BEFM nội tiếp
2)CM tứ giác BEFM là hình chữ nhật
Cho đường tròn tâm O đường kính AB. Trên cùng một nửa đường tròn (O) đường kính AB lấy hai điểm C, D sao cho cung AC nhỏ hơn cung AD. Gọi T là giao điểm của hai đường thẳng CD và AB. Vẽ đường tròn tâm I đường kính TO cắt đường tròn tâm O tại M và N (M nằm trên nửa đường tròn tâm O chứa điểm C). Gọi E là giao điểm của MN và AB. Chứng minh rằng:1. TM là tiếp tuyến của (O).2. TM2 TC. TD3. 4 điểm O, D, C, E cùng nằm trên một đường tròn.(mình cần câu 3 thôi)
Đọc tiếp
Cho đường tròn tâm O đường kính AB. Trên cùng một nửa đường tròn (O) đường kính AB lấy hai điểm C, D sao cho cung AC nhỏ hơn cung AD. Gọi T là giao điểm của hai đường thẳng CD và AB. Vẽ đường tròn tâm I đường kính TO cắt đường tròn tâm O tại M và N (M nằm trên nửa đường tròn tâm O chứa điểm C). Gọi E là giao điểm của MN và AB. Chứng minh rằng:
1. TM là tiếp tuyến của (O).
2. TM2 = TC. TD
3. 4 điểm O, D, C, E cùng nằm trên một đường tròn.
(mình cần câu 3 thôi)
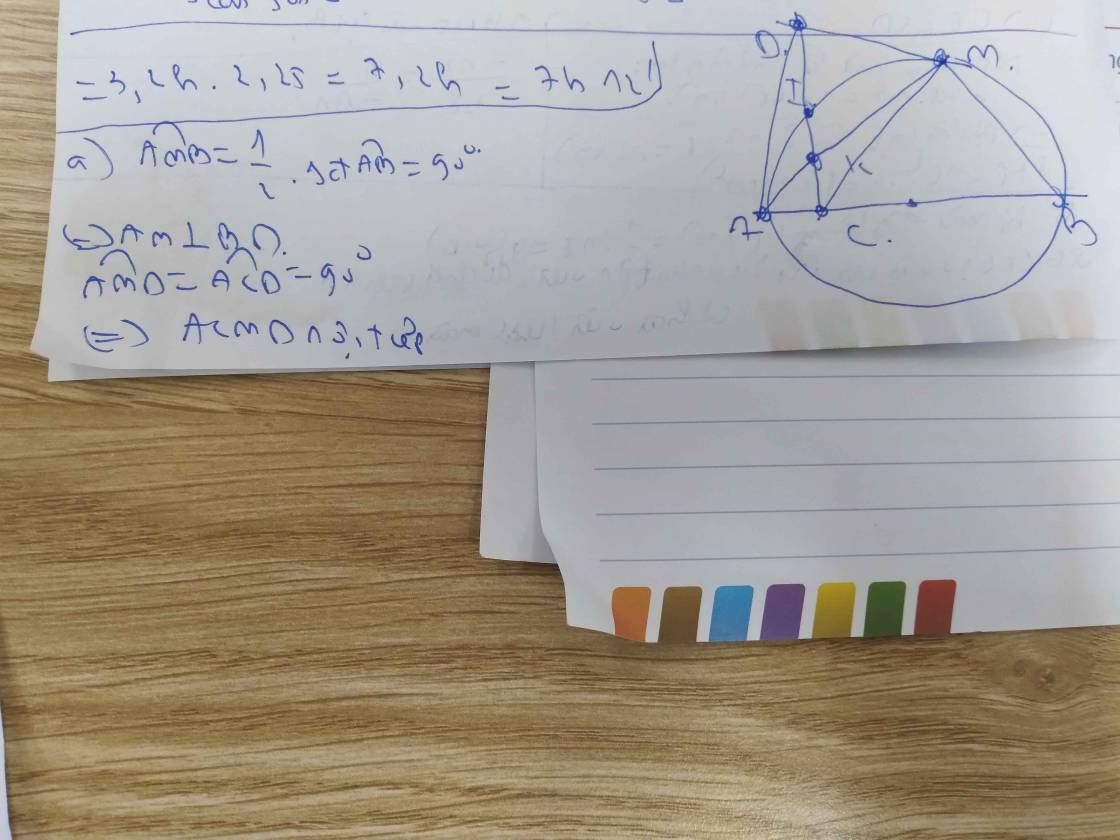
Cho nửa đường tròn tâm O đường kính AB. C là một điểm nằm giữa O và A. Đường thẳng vuông góc với AB tại C cắt nửa đường tròn trên tại I. K là một điểm bất kỳ nằm trên đoạn thẳng CI (K khác C và I), tia AK cắt nửa đường tròn (O) tại M, tia BM cắt tia CI tại D. Chứng minh: 1) Các tứ giác: ACMD; BCKM nội tiếp đường tròn. 2) CK.CD CA.CB 3) Gọi N là giao điểm của AD và đường tròn (O) chứng minh B, K, N thẳng hàng
Đọc tiếp
Cho nửa đường tròn tâm O đường kính AB. C là một điểm nằm giữa O và A. Đường thẳng vuông góc với AB tại C cắt nửa đường tròn trên tại I. K là một điểm bất kỳ nằm trên đoạn thẳng CI (K khác C và I), tia AK cắt nửa đường tròn (O) tại M, tia BM cắt tia CI tại D. Chứng minh:
1) Các tứ giác: ACMD; BCKM nội tiếp đường tròn.
2) CK.CD = CA.CB
3) Gọi N là giao điểm của AD và đường tròn (O) chứng minh B, K, N thẳng hàng
1:
góc AMB=1/2*sđ cung AB=90 độ
=>AM vuông góc BD
góc ACD=góc AMD=90 độ
=>ACMD nội tiếp
góc KCB+góc KMB=180 độ
=>BMKC nội tiếp
2: Xét ΔCAK vuông tại C và ΔCDB vuông tại C có
góc CAK=góc CDB
=>ΔCAK đồng dạng với ΔCDB
=>CA/CD=CK/CB
=>CA*CB=CD*CK
Đúng 1
Bình luận (0)
Cho nửa đường tròn tâm O đường kính AB. C là một điểm nằm giữa O và A. Đường thẳng vuông góc với AB tại C cắt nửa đường tròn trên tại I. K là một điểm bất kì nằm trên đoạn thẳng CI (K khác C và I), tia AK cắt nửa đường tròn (O) tại M, tia BM cắt CI tại D. Chứng minh :a) Các tứ giác : ACMD ; BCKM nội tiếp đường trònb) CK.CD CA.CBc) Gọi N là giao điểm của AD và (O). Chứng minh rằng : B, K, M thẳng hàng
Đọc tiếp
Cho nửa đường tròn tâm O đường kính AB. C là một điểm nằm giữa O và A. Đường thẳng vuông góc với AB tại C cắt nửa đường tròn trên tại I. K là một điểm bất kì nằm trên đoạn thẳng CI (K khác C và I), tia AK cắt nửa đường tròn (O) tại M, tia BM cắt CI tại D. Chứng minh :
a) Các tứ giác : ACMD ; BCKM nội tiếp đường tròn
b) CK.CD = CA.CB
c) Gọi N là giao điểm của AD và (O). Chứng minh rằng : B, K, M thẳng hàng
Cho nửa đường tròn tâm O đường kính AB ,C là một điểm nằm giữa O và A .Đường thẳng vuông góc với AB tại C cắt nửa đường tròn trên tại I ,K là một điểm nằm bất kì trên đoạn thẳng CI (K khác C và I) tia AK cắt nửa đường tròn O tại M tia BM cắt tia CI tại D .Chứng minh : a)Các tứ giác ACMD,BCKM nội tiếp đường tròn b)CK.CDCA.CB c) Gọi N là giao điểm của AD và đường tròn O chứng minh B,K,N thẳng hàng
Đọc tiếp
Cho nửa đường tròn tâm O đường kính AB ,C là một điểm nằm giữa O và A .Đường thẳng vuông góc với AB tại C cắt nửa đường tròn trên tại I ,K là một điểm nằm bất kì trên đoạn thẳng CI (K khác C và I) tia AK cắt nửa đường tròn O tại M tia BM cắt tia CI tại D .Chứng minh : a)Các tứ giác ACMD,BCKM nội tiếp đường tròn b)CK.CD=CA.CB c) Gọi N là giao điểm của AD và đường tròn O chứng minh B,K,N thẳng hàng
Bài IV (3,5 điểm) Cho nửa đường tròn tâm O, bán kính R, đường kính AB. Điểm C thuộc đoạn AB (C khác B;A). Trên cùng nửa mặt phẳng bờ AB có chứa nửa (O;R). Vẽ nửa đường tròn tâm I, đường kính AC và nửa đường tròn tâm J, đường kính BC. Qua C kẻ đường thẳng vuông góc với AB cắt (O;R) tại D. DA cắt nửa đường tròn tâm I tại M, DB cắt nửa đường tròn tâm J tại N 1) Chứng minh rằng: Tứ giác MDNC là hình chữ nhật2) Chứng minh rằng: Tứ giác AMNB nội tiếp.3) Chứng minh rằng: OD vuông góc MN4) Tì...
Đọc tiếp
Bài IV (3,5 điểm) Cho nửa đường tròn tâm O, bán kính R, đường kính AB. Điểm C thuộc đoạn AB (C khác B;A). Trên cùng nửa mặt phẳng bờ AB có chứa nửa (O;R). Vẽ nửa đường tròn tâm I, đường kính AC và nửa đường tròn tâm J, đường kính BC. Qua C kẻ đường thẳng vuông góc với AB cắt (O;R) tại D. DA cắt nửa đường tròn tâm I tại M, DB cắt nửa đường tròn tâm J tại N
1) Chứng minh rằng: Tứ giác MDNC là hình chữ nhật
2) Chứng minh rằng: Tứ giác AMNB nội tiếp.
3) Chứng minh rằng: OD vuông góc MN
4) Tìm vị trí của C trên AB để bán kính đường tròn ngoại tiếp tứ giác AMNB lớn nhất.
Cho nửa đường tròn tâm O, đường kính AD. Trên nửa đường tròn lấy điểm B, C ( B nằm trên cung AC). Gọi AC cắt BD tại E, kẻ EF vuông góc với AD(F thuộc AD). Chứng minh:
a) AB,DC,EF đồng quy
b) Tính AB.AP+CD.CP theo R của đường tròn tâm O đường kính AD
Cho nửa đườbg tròn tâm O , đường kính AB. Lấy OA làm đường kính của nửa đường tròn cùng nằm trên 1 nửa mặt phẳng bờ AB với nửa đường tròn (O). Trên nửa đường tròn đường kính OA lấy điểm ( C khác A; O) . Tia OC cắt đường tròn (O) tại D. Vẽ DH vuông góc với AB. Chứng minh rằng :
a, tam giác AOC = tam giác DOH
b, Tứ giác AHCD là hình thang cân
Cho điểm C nằm trên nửa đường tròn tâm O đường kính AB 2R (C khác A và B). Gọi K là trung điểm của BC. Qua B vẽ tia tiếp tuyến Bx với nửa đường tròn tâm O (tia Bx và C nằm cùng một nửa mặt phẳng có bờ AB), Bx cắt tia OK tại D. a) Chứng minh ODC ODB, từ đó suy ra DC là tiếp tuyến của đường tròn tâm O. b) Chứng minh AC.OD 2R2 c) Vẽ CH vuông góc với AB tại H, gọi I là trung điểm của CH. Tiếp tuyến tại A của đường tròn tâm O cắt tia BI tại E. Chứng minh E, C, D thẳng hàng.
Đọc tiếp
Cho điểm C nằm trên nửa đường tròn tâm O đường kính AB = 2R (C khác A và B). Gọi K là trung điểm của BC. Qua B vẽ tia tiếp tuyến Bx với nửa đường tròn tâm O (tia Bx và C nằm cùng một nửa mặt phẳng có bờ AB), Bx cắt tia OK tại D. a) Chứng minh ODC = ODB, từ đó suy ra DC là tiếp tuyến của đường tròn tâm O. b) Chứng minh AC.OD = 2R2 c) Vẽ CH vuông góc với AB tại H, gọi I là trung điểm của CH. Tiếp tuyến tại A của đường tròn tâm O cắt tia BI tại E. Chứng minh E, C, D thẳng hàng.