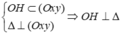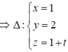Trong mặt phẳng Oxy , cho Δ ABC vuông tại A(2;3) . Đường thẳng đi qua trung điểm M của AB vuông góc với BC tại K(4;9) cắt AC tại E thỏa mãn KE = 2CK . Tìm tọa độ B,C biết hoành độ của M lớn hơn 2.
Những câu hỏi liên quan
26 tháng 3 2022 lúc 14:13
trong mặt phẳng Oxy, cho điểm I (2;-1) và đường thẳng Δ:3x+4y+3=0.Viết phương trình đường tròn tâm I cắt Δ tại hai điểm phân biệt A,B sao cho diện tích tam giác IAB = 4
gọi H là trung điểm AB
=> \(IH=d_{\left(I,\Delta\right)}=\dfrac{\left|3\cdot2+4\cdot\left(-1\right)+3\right|}{\sqrt{3^2+4^2}}=1\)
\(S_{\Delta IAB}=2\cdot\left(\dfrac{1}{2}\cdot IH\cdot HA\right)=4\)
\(IH\cdot IA=4\Leftrightarrow1\cdot HA=4\Rightarrow HA=4\)
\(\Rightarrow R=IA=\sqrt{IH^2+HA^2}=\sqrt{1^2+4^2}=\sqrt{17}\)
\(\Rightarrow\) Phương trình đường tròn (x-2)2 +(y+1)2=17
Đúng 1
Bình luận (0)
Trong mặt phẳng Oxy, cho 2 điểm a(1;3) ; b(-2;4).tìm toạ độ c sao cho tam giác ABC vuông cân tại B
Trong mặt phẳng oxy cho 2 điểm A(2;4), B(1;1) tìm tọa độ điểm C sao cho tam giác ABC vuông cân tại B
Giả sử \(C\) cần tìm có tọa độ là \(\left(x;y\right)\). Để tam giác ABC vuông cân tại B ta phải có:
\(\left\{{}\begin{matrix}\overrightarrow{BA}.\overrightarrow{BC}=0\\\left|\overrightarrow{BA}\right|=\left|\overrightarrow{BC}\right|\end{matrix}\right.\) với \(\overrightarrow{BA}=\left(1;3\right)\) và \(\overrightarrow{BC}=\left(x-1;y-1\right)\)
Điều đó có nghĩa là:
\(\left\{{}\begin{matrix}1.\left(x-1\right)+3\left(y-1\right)=0\\1^2+3^2=\left(x-1\right)^2+\left(y-1\right)^2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=4-3y\\\left(3-3y\right)^2+\left(y-1\right)^2=10\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=4-3y\\10y^2-20y=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=4\\y=0\end{matrix}\right.\\\left\{{}\begin{matrix}x=-2\\y=2\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}C\left(4;0\right)\\C\left(-2;2\right)\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Trong không gian Oxyz, cho mặt phẳng (α): 2x + y -2z – 2 – 0, đường thẳng
d
:
x
+
1
1
y
+
2
2
z
+
3
2
và điểm
A
1
2
;...
Đọc tiếp
Trong không gian Oxyz, cho mặt phẳng (α): 2x + y -2z – 2 – 0, đường thẳng d : x + 1 1 = y + 2 2 = z + 3 2 và điểm A 1 2 ; 1 ; 1 . Gọi Δ là đường thẳng nằm trong mặt phẳng (α), song song với d đồng thời cách d một khoảng bằng 3. Đường thẳng Δ cắt mặt phẳng (Oxy) tại điểm B. Độ dài đoạn thẳng AB bằng.
A. 7/2
B. √21/2
C. 7/3
D. 3/2
Chọn A
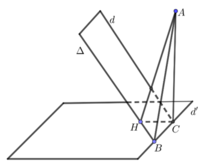
Cách 1: Ta có: B ∈ Oxy và B ∈ (α) nên B (a ; 2 – 2a ; 0).
đi qua M (-1 ; -2 ; -3) và có một véctơ chỉ phương là 
Ta có: d ⊂ (α) nên d và Δ song song với nhau và cùng nằm trong mặt phẳng (α).
Gọi C = d ∩ (Oxy) nên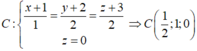 
Gọi d’ = (α) ∩ (Oxy), suy ra d’ thỏa hệ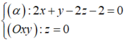 
Do đó, d’ qua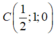 
và có VTCP 
Gọi φ = (Δ, d’) = (d, d’)
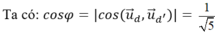
Gọi H là hình chiếu của C lên Δ. Ta có CH = 3 và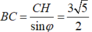 
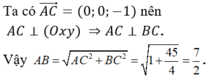
Cách 2: Ta có: 
đi qua M (-1 ; -2 ; -3) và có một VTCP là 
Ta có: B = Δ ∩ (Oxy), Δ ⊂ (α) nên B ∈ (Oxy) ∩ (α) => B (a; 2 – a; 0)
Ta có: Δ // d và d (Δ, d) = 3 nên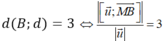 
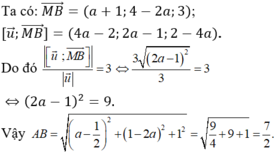
Đúng 0
Bình luận (0)
Trong không gian Oxyz, đường thẳng Δ qua điểm M(1−2m;2+ m;1) và vuông góc với mặt phẳng (Oxy) sao cho khoảng cách từ gốc toạ độ O đến đường thẳng Δ nhỏ nhất có phương trình là A.
x
1
y
2
z...
Đọc tiếp
Trong không gian Oxyz, đường thẳng Δ qua điểm M(1−2m;2+ m;1) và vuông góc với mặt phẳng (Oxy) sao cho khoảng cách từ gốc toạ độ O đến đường thẳng Δ nhỏ nhất có phương trình là
A. x = 1 y = 2 z = 1 + t
B. x = 1 + t y = 2 + t z = 1
C. x = 5 y = 0 z = 1 + t
D. x = 3 y = 1 z = 1 + t
1.Trong mặt phẳng hệ tọa độ Oxy, viết phương trình đường thẳng Δ qua M(1,2) cắt Ox tại A, cắt Oy tại B sao cho OA+OB =12 2.Cho 3 điểm A(2,0), B(3,4), C(1,1), Viết phương trình đưởng thẳng qua C cách đều hai điểm A, B 3.Trong hệ tọa độ Oxy cho tam giác ABC có BC= x+y=9=0, đường cao B, C lần lượt là: d1: x+2y-13=0, d2:7x=5y-49=0. Tìm tọa độ điểm A
Trong mặt phẳng Oxy cho 2 điểm A(4;0), B(0;-2). Tìm tọa độ tâm đường tròn ngoại tiếp Δ OAB
Ta thấy A,B một điểm thì thuộc trục tung, một điểm thì thuộc trục hoành nên tam giác OAB vuông tại O
=> Tâm đường tròn ngoại tiếp là trung điểm của AB
có tọa độ (2; -1)
Đúng 1
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho hai điểm A(2; 4) và B(1; 1). Tìm tọa độ điểm C sao cho tam giác ABC vuông cân tại B?
A. C(4; 0)
B.C(- 2; 2)
C. C(4; 0); C( -2; 2)
D. C(2; 0)
Gọi C(x, y).
Ta có B A → = 1 ; 3 B C → = x − 1 ; y − 1 .
Tam giác ABC vuông cân tại B:
⇔ B A → . B C → = 0 B A = B C ⇔ 1. x − 1 + 3. y − 1 = 0 1 2 + 3 2 = x − 1 2 + y − 1 2
⇔ x = 4 − 3 y 10 y 2 − 20 y = 0 ⇔ y = 0 x = 4 hay y = 2 x = − 2 .
Chọn C.
Đúng 0
Bình luận (0)
Trong mặt phẳng toạ độ Oxy, cho 2 điểm A(-2,4) và B(8,4). Tìm toạ độ điểm C thuộc trục hoành sao cho tam giác ABC vuông tại C
Do C thuôc trục hoành nên tọa độ có dạng \(C\left(c;0\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AC}=\left(c+2;-4\right)\\\overrightarrow{BC}=\left(c-8;-4\right)\end{matrix}\right.\)
Do tam giác ABC vuông tại C \(\Rightarrow\overrightarrow{AC}.\overrightarrow{BC}=0\)
\(\Rightarrow\left(c+2\right)\left(c-8\right)+16=0\)
\(\Rightarrow c^2-6c=0\Rightarrow\left[{}\begin{matrix}c=0\\c=6\end{matrix}\right.\)
Vậy có 2 điểm C thỏa mãn là \(C\left(0;0\right)\) và \(C\left(6;0\right)\)
Đúng 0
Bình luận (0)
Trong mặt phẳng toạ độ Oxy, cho 2 điểm A(1,2) và B(-3,1). Tìm toạ độ điểm C thuộc trục tung sao cho tam giác ABC vuông tại A. Tính diện tích tam giác ABC
Do C thuộc trục tung nên tọa độ có dạng \(C\left(0;c\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(-4;-1\right)\\\overrightarrow{AC}=\left(-1;c-2\right)\end{matrix}\right.\)
Do tam giác ABC vuông tại A \(\Rightarrow\overrightarrow{AB}.\overrightarrow{AC}=0\)
\(\Rightarrow4-\left(c-2\right)=0\Rightarrow c=6\)
\(\Rightarrow C\left(0;6\right)\)
\(\Rightarrow\overrightarrow{AC}=\left(-1;4\right)\Rightarrow\left\{{}\begin{matrix}AB=\sqrt{\left(-4\right)^2+\left(-1\right)^2}=\sqrt{17}\\AC=\sqrt{\left(-1\right)^2+4^2}=\sqrt{17}\end{matrix}\right.\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}AB.AC=\dfrac{17}{2}\)
Đúng 0
Bình luận (0)