Trong không gian Oxyz, cho hai điểm \(A\left(2;0;0\right);B\left(0;0;8\right)\) và điểm C sao cho \(\overrightarrow{AC}=\left(0;6;0\right)\)
Tính khoảng cách từ trung điểm I của BC đến đường OA ?
Những câu hỏi liên quan
Trong không gian Oxyz, cho hai điểm A(2; 0; 1), B(-1; 2; 3). Tính khoảng cách giữa hai điểm AB
A. A B = 17
B. A B = 13
C. A B = 14
D. A B = 19
14 tháng 4 2022 lúc 0:02
Trong không gian Oxyz, cho đường thẳng d:dfrac{x-1}{2}dfrac{y-2}{2}dfrac{z}{1} và hai điểm Aleft(1;-1;1right), Bleft(4;2;-2right). Gọi Δ là đường thẳng đi qua A và vuông góc với d sao cho khoảng cách từ điểm B đến Δ là nhỏ nhất. Phương trình đường thẳng Δ là:A. dfrac{x-1}{-1}dfrac{y+1}{1}dfrac{z-1}{4} B. dfrac{x-1}{1}dfrac{y+1}{1}dfrac{z-1}{4}C. dfrac{x-1}{1}dfrac{y+1}{-1}dfrac{z-1}{4} D. dfrac{x-1}{1}dfrac{y+1}{1}dfrac{z-1}{-4}
Đọc tiếp
Trong không gian Oxyz, cho đường thẳng \(d:\dfrac{x-1}{2}=\dfrac{y-2}{2}=\dfrac{z}{1}\) và hai điểm \(A\left(1;-1;1\right)\), \(B\left(4;2;-2\right)\). Gọi Δ là đường thẳng đi qua \(A\) và vuông góc với \(d\) sao cho khoảng cách từ điểm \(B\) đến Δ là nhỏ nhất. Phương trình đường thẳng Δ là:
A. \(\dfrac{x-1}{-1}=\dfrac{y+1}{1}=\dfrac{z-1}{4}\) B. \(\dfrac{x-1}{1}=\dfrac{y+1}{1}=\dfrac{z-1}{4}\)
C. \(\dfrac{x-1}{1}=\dfrac{y+1}{-1}=\dfrac{z-1}{4}\) D. \(\dfrac{x-1}{1}=\dfrac{y+1}{1}=\dfrac{z-1}{-4}\)
Mặt phẳng (P) qua A và vuông góc d có phương trình:
\(2\left(x-1\right)+2\left(y+1\right)+1\left(z-1\right)=0\)
\(\Leftrightarrow2x+2y+z-1=0\)
Đường thẳng d' song song d và đi qua B (nên d' vuông góc (P)) có dạng:
\(\left\{{}\begin{matrix}x=4+2t\\y=2+2t\\z=-2+t\end{matrix}\right.\)
\(\Rightarrow\) Giao điểm C của d' và (P) thỏa mãn:
\(2\left(4+2t\right)+2\left(2+2t\right)-2+t-1=0\Rightarrow t=-1\Rightarrow C\left(2;0;-3\right)\)
\(\Rightarrow\overrightarrow{AC}=\left(1;1;-4\right)\Rightarrow\) là 1 vtcp của \(\Delta\Rightarrow\) D là đáp án đúng
Đúng 1
Bình luận (4)
Trong không gian Oxyz, cho hai điểm A(1;-1;2) và B(2;1;1). Tính
A
B
→
2
A. 2 B. 6 C.
2
D.
6
Đọc tiếp
Trong không gian Oxyz, cho hai điểm A(1;-1;2) và B(2;1;1). Tính A B → 2
A. 2
B. 6
C. 2
D. 6
Trong không gian Oxyz, cho hai điểm A(-2;-1;3), B(0;3;1). Gọi ( α ) là mặt phẳng
A. (2;4;1)
B. (1;2;-1)
C. (-1;1;2)
D. (1;0;1)
Trong không gian Oxyz, cho hai điểm
A
(
1
;
2
;
1
)
,
B
(
2
;
-
1
;
2
)
.
Điểm M trên trục và cách đều hai điểm A, B có tọa độ là A.
M
1
2
;
0
;
0
B.
M...
Đọc tiếp
Trong không gian Oxyz, cho hai điểm A ( 1 ; 2 ; 1 ) , B ( 2 ; - 1 ; 2 ) . Điểm M trên trục và cách đều hai điểm A, B có tọa độ là
A. M 1 2 ; 0 ; 0
B. M - 1 2 ; 0 ; 0
C M 3 2 ; 0 ; 0
D. M 0 ; 1 2 ; 3 2
Chọn C.
Do điểm M thuộc trục Ox nên M(a;0;0)
Vì M cách đều hai điểm A, B nên MA = MB hay
Ta có:
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A (-2; 2; -2); B(3; -3; 3). Điểm M trong không gian thỏa mãn MA/MB 2/3. Khi đó độ dài OM lớn nhất bằng: A. 6
3
B. 12
3
C.
5
3
2
D. 5
3
Đọc tiếp
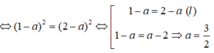
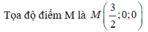
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A (-2; 2; -2); B(3; -3; 3). Điểm M trong không gian thỏa mãn MA/MB = 2/3. Khi đó độ dài OM lớn nhất bằng:
A. 6 3
B. 12 3
C. 5 3 2
D. 5 3
Chọn B
Gọi M (x; y; z)
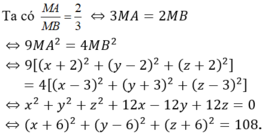
Như vậy, điểm M thuộc mặt cầu (S) tâm I(-6;6;-6) và bán kính R = √108 = 6√3. Do đó OM lớn nhất bằng
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho hai điểm
A
(
1
;
2
;
1
)
,
B
(
2
;
-
1
;
2
)
.
Điểm M trên trục Ox và cách đều hai điểm A, B có tọa độ là A.
M
1
2
;
0
;
0
B.
M...
Đọc tiếp
Trong không gian Oxyz, cho hai điểm A ( 1 ; 2 ; 1 ) , B ( 2 ; - 1 ; 2 ) . Điểm M trên trục Ox và cách đều hai điểm A, B có tọa độ là
A. M 1 2 ; 0 ; 0
B. M - 1 2 ; 0 ; 0
C. M 3 2 ; 0 ; 0
D. M 0 ; 1 2 ; 3 2
Chọn C.
Do điểm M thuộc trục Ox nên M(a,0,0)
Vì M cách đều hai điểm A, B nên MA = MB hay
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho hai điểm
A
(
1
;
2
;
1
)
,
B
(
2
;
-
1
;
2
)
.
Điểm M trên trục Ox và cách đều hai điểm A, B có tọa độ là A.
M
1
2
;
0
;
0
B.
M
-...
Đọc tiếp
Trong không gian Oxyz, cho hai điểm A ( 1 ; 2 ; 1 ) , B ( 2 ; - 1 ; 2 ) . Điểm M trên trục Ox và cách đều hai điểm A, B có tọa độ là
A. M 1 2 ; 0 ; 0
B. M - 1 2 ; 0 ; 0
C. M 3 2 ; 0 ; 0
D. M 0 ; 1 2 ; 3 2
Chọn C.
Do điểm M thuộc trục Ox nên M(a,0,0)
Vì M cách đều hai điểm A, B nên MA = MB hay
Đúng 0
Bình luận (0)
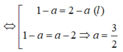
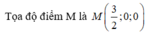
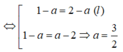
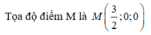
Trong không gian Oxyz, cho hai điểm A(1;-3;1), B(3;0;-2). Tính độ dài đoạn AB
A. 22
B. 22
C. 26
D. 26
15 tháng 4 2022 lúc 21:37
Trong không gian tọa độ Oxyz cho đường thẳng d:dfrac{x-1}{2}dfrac{y-1}{2}dfrac{z+1}{1} và hai điểm Aleft(6;0;0right), Bleft(0;0;-6right). Khi điểm M thay đổi trên đường thẳng d, hãy tìm giá trị nhỏ nhất của biểu thức PMA+MBA. minP6sqrt{3} B. minP6sqrt{2} C. minP9 D. minP12Mình cần bài giải ạ, mình cảm ơn nhiều♥
Đọc tiếp
Trong không gian tọa độ \(Oxyz\) cho đường thẳng \(d:\dfrac{x-1}{2}=\dfrac{y-1}{2}=\dfrac{z+1}{1}\) và hai điểm \(A\left(6;0;0\right)\), \(B\left(0;0;-6\right)\). Khi điểm \(M\) thay đổi trên đường thẳng \(d\), hãy tìm giá trị nhỏ nhất của biểu thức \(P=MA+MB\)
A. \(minP=6\sqrt{3}\) B. \(minP=6\sqrt{2}\) C. \(minP=9\) D. \(minP=12\)
Mình cần bài giải ạ, mình cảm ơn nhiều♥
Phương trình d dạng tham số: \(\left\{{}\begin{matrix}x=1+2t\\y=1+2t\\z=-1+t\end{matrix}\right.\)
Gọi \(M\left(1+2t;1+2t;-1+t\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AM}=\left(2t-5;2t+1;t-1\right)\\\overrightarrow{BM}=\left(2t+1;2t+1;t+5\right)\end{matrix}\right.\)
\(\Rightarrow P=\sqrt{\left(2t-5\right)^2+\left(2t+1\right)^2+\left(t-1\right)^2}+\sqrt{\left(2t+1\right)^2+\left(2t+1\right)^2+\left(t+5\right)^2}\)
\(=\sqrt{9t^2-18t+27}+\sqrt{9t^2+18t+27}\)
\(=\sqrt{\left(3-3t\right)^2+18}+\sqrt{\left(3+3t\right)^2+18}\)
\(\ge\sqrt{\left(3-3t+3+3t\right)^2+4.18}=6\sqrt{3}\)
Đúng 2
Bình luận (0)