Cho hình chữ nhật ABCD. Biết các đỉnh A(5; 1), C(0; 6) và phương trình CD: x + 2y -12 = 0. Tìm phương trình đường thẳng chứa các cạnh còn lại.

Những câu hỏi liên quan
Cho hình chữ nhật ABCD có đỉnh A(-1;2) và tâm O(0;0). Xác định tọa độ các đỉnh còn lại của hình chữ nhật ABCD, biết đường thẳng BC đi qua điểm M(1;4) a) Tìm tọa độ C. b) Viết pt đt BC. c) Tim tọa độ các điểm B, D.
trong mặt phẳng với hệ tọa độ Oxy, cho hình chữ nhật ABCD có đỉnh A(-1,2) và tâm I(1/2:0) xác định tọa độ các đỉnh còn lại của hình chữ nhật ABCD, biết đường thẳng BC đi qua điểm m(4;-3)
I là trung điểm AC \(\Rightarrow C\left(2;-2\right)\)
\(\Rightarrow\overrightarrow{CM}=\left(2;-1\right)\Rightarrow\) đường thẳng BC có dạng:
\(1\left(x-2\right)+2\left(y+2\right)=0\Leftrightarrow x+2y+2=0\)
Đường thẳng AB qua A và vuông góc BC nên nhận \(\left(2;-1\right)\) là 1 vtpt
Phương trình AB:
\(2\left(x+1\right)-1\left(y-2\right)=0\Leftrightarrow2x-y+4=0\)
B là giao điểm AB và BC nên tọa độ là nghiệm:
\(\left\{{}\begin{matrix}x+2y+2=0\\2x-y+4=0\end{matrix}\right.\) \(\Rightarrow B\left(...\right)\)
I là trung điểm BD \(\Rightarrow\left\{{}\begin{matrix}x_D=2x_I-x_B=...\\y_D=2y_I-y_B=...\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Cho hình chữ nhật ABCD. Qua một điểm M tùy ý nằm ở bên trong hình chữ nhật đó, kẻ các đường thẳng song song với các hình chữ nhật, chia hình chữ nhật thành 4 hình chữ nhật nhỏ. CMR ít nhất một trong hai hình chữ nhật nhỏ chứa đỉnh A hoặc đỉnh C có diện tích không vượt quá 1/4 diện tích hình chữ nhật ABCD
Trong mặt phẳng hệ tọa độ Oxy , cho hình chữ nhật ABCD tâm O. Biết phương trình đường thẳng AB:x--y+5=0 và trung điểm M của cạnh BC thuộc đường thẳng x+3y-6=0, xác định tọa độ các đỉnh của hình chữ nhật ABCD
Phương trình đường thẳng qua O và song song AB có dạng:
Tọa độ M là nghiệm của hệ:
Phương trình đường thẳng BC qua M, nhận là 1 vtpt có dạng:
Tọa độ B là nghiệm của hệ:
M là trung điểm BC tọa độ C
O là trung điểm AC tọa độ A
O là trung điểm BD
Đúng 2
Bình luận (0)
Cho hình chữ nhật ABCD . Trên cạnh AB lấy 5 điểm và trên cạnh CD lấy 6 điểm . Nối đỉnh C và đỉnh D với mỗi điểm thuộc cạnh AB. Nối đỉnh A và đỉnh B với mỗi điểm thuộc cạnh CD . Hỏi có bao nhiêu tam giác có các đỉnh nằm trên các cạnh của hình chữ nhật được tạo thành
Cho hình chữ nhật ABCD có chiều dài 12 cm, chiều rộng 5 cm. Nối đỉnh A với trung điểm N của cạnh DC. Nối đỉnh C với trung điểm M của cạnh AB. Cho biết hình tứ giác AMCN là hình bình hành có chiều cao MN bằng chiều rộng của hình chữ nhật.a) Giải thích tại sao AN và Mc song song và bằng nhau.b) Diện tích hình chữ nhật ABCD gấp mấy lần diện tích hình bình hành AMCN?
Đọc tiếp
Cho hình chữ nhật ABCD có chiều dài 12 cm, chiều rộng 5 cm. Nối đỉnh A với trung điểm N của cạnh DC. Nối đỉnh C với trung điểm M của cạnh AB. Cho biết hình tứ giác AMCN là hình bình hành có chiều cao MN bằng chiều rộng của hình chữ nhật.
a) Giải thích tại sao AN và Mc song song và bằng nhau.
b) Diện tích hình chữ nhật ABCD gấp mấy lần diện tích hình bình hành AMCN?
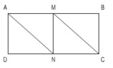
a) Hai đoạn thẳng AN và MC song song và bằng nhau vì chúng là hai cạnh đối diện của hình bình hành AMCN.
b) Diện tích hình chữ nhật ABCD là:
12 × 5 = 60 ( c m 2 )
Vì N là trung điểm của DC nên NC dài :
12 ∶ 6 = 6 cm
Diện tích hình bình hành AMCN là :
6 × 5 = 30( c m 2 )
So với diện tích hình bình hành AMCN thì diện tích hình chữ nhật ABCD gấp: 60 : 20 = 2 lần
Nói thêm : Có thể giải câu b gấp đôi đồ dài đáy hình bình hành.
Chiều rộng hình chữ nhật ABCD gắp đôi bộ dài đáy hình bình hành.
Chiều rộng hình chữ nhật ABCD bằng chiều cao hình bình hành.
Vậy diện tích hình chữ nhật gập đôi diện tích hình bình hành.
Cách 3 :
Đường gấp khúc AMNC chia hình chữ nhật ABCD thành 4 tam giác (vuông) bằng nhau. Hình bình hành AMNC gồm 2 tam giác ấy. Vậy diện tích hình chữ nhật ABCD gấp đôi diện tích hình bình hành AMCN.
Đúng 0
Bình luận (0)
Cho hình chữ nhật ABCD có chiều dài 12 cm, chiều rộng 5 cm. Nối đỉnh A với trung điểm N của cạnh DC. Nối đỉnh C với trung điểm M của cạnh AB. Cho biết hình tứ giác AMCN là hình bình hành có chiều cao MN bằng chiều rộng của hình chữ nhật.a) Giải thích tại sao AN và Mc song song và bằng nhau.b) Diện tích hình chữ nhật ABCD gấp mấy lần diện tích hình bình hành AMCN ?
Đọc tiếp
Cho hình chữ nhật ABCD có chiều dài 12 cm, chiều rộng 5 cm. Nối đỉnh A với trung điểm N của cạnh DC. Nối đỉnh C với trung điểm M của cạnh AB. Cho biết hình tứ giác AMCN là hình bình hành có chiều cao MN bằng chiều rộng của hình chữ nhật.
a) Giải thích tại sao AN và Mc song song và bằng nhau.
b) Diện tích hình chữ nhật ABCD gấp mấy lần diện tích hình bình hành AMCN ?
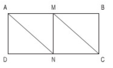
a) Hai đoạn thẳng AN và MC song song và bằng nhau vì chúng là hai cạnh đối diện của hình bình hành AMCN.
b) Diện tích hình chữ nhật ABCD là:
12 × 5 = 60 (cm2)
Vì N là trung điểm của DC nên NC dài :
12 ∶ 2 = 6 cm
Diện tích hình bình hành AMCN là :
6 × 5 = 30(cm2)
So với diện tích hình bình hành AMCN thì diện tích hình chữ nhật ABCD gấp : 60 : 20 = 2 lần
Nói thêm : Có thể giải câu b gấp đôi đồ dài đáy hình bình hành.
Chiều rộng hình chữ nhật ABCD gắp đôi bộ dài đáy hình bình hành.
Chiều rộng hình chữ nhật ABCD bằng chiều cao hình bình hành.
Vậy diện tích hình chữ nhật gập đôi diện tích hình bình hành.
Cách 3 :
Đường gấp khúc AMNC chia hình chữ nhật ABCD thành 4 tam giác ( vuông) bằng nhau. Hình bình hành AMNC gồm 2 tam giác ấy. Vậy diện tích hình chữ nhật ABCD gấp đôi diện tích hình bình hành AMCN.
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD. Ba đỉnh A, B, C biểu diễn các số phức a = 2 - 2i; b = -1 + i và c = 5 + ki với k ∈ R . Tìm k để ABCD là hình chữ nhật
A. k = 5
B. k = 6
C. k = 7
D. k = 8
Ta có ABCD là hình bình hành
⇔ C D → = B A → ⇔ d - c = a - b ⇔ d = a + c - b ⇔ d = 8 + m - 3 i
ABCD là hình chữ nhật
⇔ A V = B D ⇔ c - a = d - b ⇔ 3 + m + 2 i = 9 + m - 4 i ⇔ 3 2 + m + 2 2 = 9 2 + m - 4 2 ⇔ m = 7
Đáp án C
Đúng 0
Bình luận (0)
Cho hình chữ nhật ABCD có đỉnh A(7; 4) và phương trình hai cạnh là: 7x – 3y + 5 = 0, 3x + 7y – 1 = 0. Diện tích hình chữ nhật ABCD là:
A. 2016/29
B. 2016 58
C. 1008 58
D.1008/29
Ta kiểm tra thấy đỉnh A(7; 4) không nằm trên các đường thẳng d 1 : 7 x − 3 y + 5 = 0 , d 2 : 3 x + 7 y − 1 = 0 nên đây là các cạnh CB, CD. Ta có
S = d A , B C . d A , C D = 7.7 − 3.4 + 5 7 2 + − 3 2 . 3.7 + 7.4 − 1 3 2 + 7 2 = 1008 29
ĐÁP ÁN D
Đúng 0
Bình luận (0)









