5:

Gọi (d): y=ax+b là phương trình cần tìm

Theo đề, ta có hệ:
3a+b=-1 và 2a+b=3

=>a=-4 và b=11

=>y=-4x+11

4:

vecto BC=(1;-1)

=>AH có VTPT là (1;-1)

Phương trình AH là:

1(x-1)+(-1)(y+3)=0

=>x-1-y-3=0

=>x-y-4=0

Đường thẳng d có 1 vtcp là (1;-3) nên nhận (3;1) là 1 vtpt

Phương trình d:

\(3\left(x+2\right)+1\left(y-3\right)=0\Leftrightarrow3x+y+3=0\)

ĐÁP ÁN C

Do đường thẳng ∆ song song với đường thẳng 2x – y + 3= 0 nên đường thẳng ∆ có dạng:

2x  - y +  c= 0  ( c     ≠ 3 ) ​

Do đường thẳng ∆ đi qua  M( 3; 4) nên ta có:

 2. 3 -  4 + c =0  ⇔ c = − 2

Vậy phương trình của ∆ là  2x – y – 2 = 0

Chọn D.

Phương trình tổng quát của đường thẳng Δ đi qua điểm M(-1;2) và có hệ số góc k = 3 là: y = 3(x + 1) + 2 ⇔ 3x - y + 5 = 0

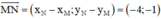
Đường thẳng MN nhận 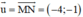 là 1 vtcp

⇒ MN nhận 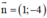 là 1 vtpt

Mà M(4; 0) thuộc đường thẳng MN

⇒ Phương trình đường thẳng MN: 1(x - 4) – 4(y - 0) = 0 hay x – 4y – 4 = 0.

Đáp án: C

Phương trình tổng quát của đường thẳng d đi qua M(2;-3) và nhận  n → = 3 ; - 2  làm vecto pháp tuyến có dạng:

3(x - 2) - 2(y + 3) = 0 ⇔ 3x - 2y - 12 = 0

\(\Delta\left\{{}\begin{matrix}quaM\left(-2;3\right)\\VTCP=\overrightarrow{u}=\overrightarrow{MN}=\left(6;-2\right)\end{matrix}\right.\)

\(\Rightarrow\overrightarrow{VTPT}=\overrightarrow{n}=\left(2;6\right)\)

\(PTTQ\) của \(\Delta:a\left(x-x_o\right)+b\left(y-y_o\right)=0\)

\(\Leftrightarrow2\left(x+2\right)+6\left(y-3\right)=0\)

\(\Leftrightarrow2x+4+6y-18=0\)

\(\Leftrightarrow2x+6y-14=0\)

Vậy PTTQ của đường thẳng \(\Delta\) là : \(2x+6y-14=0\)

Ta có:

Vecto MN = (6; -2) = (3; -1) là vec tơ chỉ phương của (MN)

⇒ Vec tơ pháp tuyến của (MN) là n = (2; 6) = (1; 3)

Phương trình tổng quát của (MN):

(MN): 1.(x + 2) + 3(y - 3) = 0

⇔ x + 7 + 3y - 9 = 0

⇔ x + 3y - 7 = 0

a: (d): 2x-y+3=0

=>y=2x+3

Vì (d') vuông góc với (d) nên 2a=-1

=>a=-1/2

Vậy: (d'): y=-1/2x+b

Thay x=3 và y=1 vào (d'), ta được:

b-3/2=1

hay b=5/2

Vậy: (d'): y=-1/2x+5/2

b: Tọa độ giao điểm là:

\(\left\{{}\begin{matrix}2x+3=-\dfrac{1}{2}x+\dfrac{5}{2}\\y=2x+3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{5}{2}x=-\dfrac{1}{2}\\y=2x+3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{5}\\y=-\dfrac{2}{5}+3=\dfrac{13}{5}\end{matrix}\right.\)

Đề bài đúng là Cho phương trình (d) có pt tổng quát : 2x-y+3=0 và điểm M( 3,1)