Trong hệ trục tọa độ Oxyz, cho tứ diện ABCD biết A(3;-2;m), B(2;0;0), C(0;4;0), D(0;0;3). Tìm giá trị dương của tham số m để thể tích tứ diện bằng 8.
A. m=8
B. m=4
C. m=12
D. m=6
Những câu hỏi liên quan
Trong không gian với hệ trục tọa độ Oxyz, cho tứ diện ABCD với
A
0
;
1
;
1
,
B
0
;
2
;
1
,
C
−
1
;
0
;
2
,...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho tứ diện ABCD với A 0 ; 1 ; 1 , B 0 ; 2 ; 1 , C − 1 ; 0 ; 2 , D − 3 ; 2 ; 5 . Tính thể tích tứ diện ABCD.
A. 1 6
B. 1
C. 1 3
D. 1 2
Trong không gian với hệ trục tọa độ Oxyz, cho bốn điểm A, B, C,D. Tâm I của mặt cầu ngoại tiếp tứ diện ABCD có tọa độ là: A. (3/2;-3/2;3/2) B. (3/2;3/2;3/2) C. (-3/2;3/2;3/2) D. (3/2;3/2;-3/2)
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho bốn điểm A, B, C,D. Tâm I của mặt cầu ngoại tiếp tứ diện ABCD có tọa độ là:
A. (3/2;-3/2;3/2)
B. (3/2;3/2;3/2)
C. (-3/2;3/2;3/2)
D. (3/2;3/2;-3/2)
Trong hệ tọa độ Oxyz cho ba điểm
A
-
3
;
4
;
0
,
B
6
;
-
2
;
1
,
C
3
;
0
;
2
. Có bao nhiêu điểm D...
Đọc tiếp
Trong hệ tọa độ Oxyz cho ba điểm A - 3 ; 4 ; 0 , B 6 ; - 2 ; 1 , C 3 ; 0 ; 2 . Có bao nhiêu điểm D thuộc một trong ba trục tọa độ mà thể tích tứ diện ABCD bằng 2017?
trong hệ trục tọa độ oxyz cho 4 điểm A(1;-2;0), B(2;0;3), C(-2;1;3) và D(0;1;1) thể tích khối tứ diện ABCD bằng A.6 B.8 C.12 D.4
\(\overrightarrow{AB}=\left(1;2;3\right)\) ; \(\overrightarrow{AC}=\left(-3;3;3\right)\) ; \(\overrightarrow{AD}=\left(-1;3;1\right)\)
\(V_{ABCD}=\dfrac{1}{6}\left|\left[\overrightarrow{AB};\overrightarrow{AC}\right].\overrightarrow{AD}\right|=4\)
Đúng 0
Bình luận (0)
Trong không gian với hệ trục tọa độ Oxyz ,cho tứ diện ABCD có tọa độ các điểm A(1;1;1), B(2;0;2), C(-1;-1;0), D(0;3;4). Trên các cạnh AB, AC, AD lần lượt lấy các điểm B,C, D sao cho
A
B
A
B
+
A
C
A
C...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz ,cho tứ diện ABCD có tọa độ các điểm A(1;1;1), B(2;0;2), C(-1;-1;0), D(0;3;4). Trên các cạnh AB, AC, AD lần lượt lấy các điểm B',C', D' sao cho A B A B ' + A C A C ' + A D A D ' = 4 và tứ diện AB'C'D' có thể tích nhỏ nhất. Phương trình mặt phẳng (B'C'D') là
A. 16x-40y-44z+39=0
B. 16x-40y-44z-39=0
C. 16x+40y+44z-39=0
D. 16x+40y-44z+39=0
Chọn D
Trên cạnh AB, AC , AD của tứ diện ABCD lần lượt có các điểm B', C', D'. Áp dụng công thức tỷ số thể tích ta có
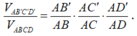
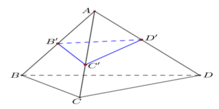
Từ giả thiết
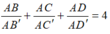
áp dụng bất đẳng thức AM- GM ta có
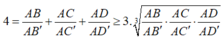
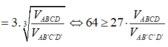
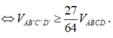
Do thể tích ABCD cố định nên thể tích AB'C'D' nhỏ nhất
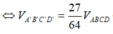
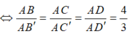
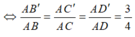
=> (B'C'D') song song với (BCD) và đi qua điểm B'
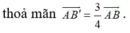
suy ra vectơ pháp tuyến của mặt phẳng (B'C'D') là:
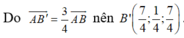
Vậy phương trình (B'C'D') là:
Đúng 0
Bình luận (0)
Trong không gian với hệ trục tọa độ Oxyz, cho tứ diện ABCD có điểm A(1;1;1) , B(2;0;2), C(-1; -1; 0), D(0;3;4) Trên các cạnh AB, AC, AD lần lượt lấy các điểm B, C, D thỏa:
A
B
A
B
+
A
C
A
C
+
A
D...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho tứ diện ABCD có điểm A(1;1;1) , B(2;0;2), C(-1; -1; 0), D(0;3;4) Trên các cạnh AB, AC, AD lần lượt lấy các điểm B', C', D' thỏa: A B A B ' + A C A C ' + A D A D ' = 4 Viết phương trình mặt phẳng (B'C'D') biết tứ diện AB'C'D' có thể tích nhỏ nhất?
A. 16x+40y+44z-39=0
B. 16x+40y-44z+39=0
C. 16x-40y-44z+39=0
D. 16x-40y-44z-39=0
Chọn C
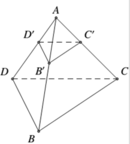
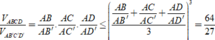
Dấu = xảy ra khi:
Suy ra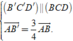 
Ta có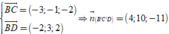 
Mặt khác
Vậy phương trình mặt phẳng (B' C' D') là 
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz cho tứ diện ABCD với
A
2
;
1
;
-
1
,
B
3
;
0
;
1
,
C
2
;
-
1
;...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho tứ diện ABCD với A 2 ; 1 ; - 1 , B 3 ; 0 ; 1 , C 2 ; - 1 ; 3 , điểm D thuộc Oy và thể tích của tứ diện ABCD bằng 5. Tọa độ của đỉnh D là
A. D(0;-7;0)
B. D(0;8;0)
C. D(0;-7;0) hoặc D(0;8;0)
D. D(0;7;0) hoặc D(0;-8;0)
Trong không gian với hệ tọa độ Oxyz cho bốn điểm A(1;0;2), B(-2;1;3), C(3;2;4), D(6;9;-5). Tọa độ trọng tâm của tứ diện ABCD là
A. (2;3;1).
B. (2;3;-1).
C. (-2;3;1).
D. (2;-3;1).
Trong không gian với hệ tọa độ Oxyz cho bốn điểm
A(1;0;2),B(-2;1;3),C(3;2;4),D(6;9;-5).Tọa độ trọng tâm của tứ diện ABCD là:
A. (2;3;1)
B. (2;3;-1)
C. (-2;3;1)
D. (2;-3;1)
