Tiếp tuyến kẻ từ điểm (2; 3) tới đồ thị hàm số y = 3 x + 4 x - 1 là
A. y = -28x+59; y = x+1
B. y = -24x+51; y = x+1
C. y = -28x+59
D. y = 28x+59; y = x+51
Những câu hỏi liên quan
cho nửa đường tròn (O) đường kính AB=2R trên tia đối của tia AB lấy điểm E (E≠A) từ E kẻ tiếp tuyến EM với nửa đường tròn ( M là tiếp điểm) tiếp tuyến kẻ từ E cắt 2 tiếp tuyến kẻ từ A và B theo thứ tự tại C và D
a) Chứng minh CD=AC+BD
Xem chi tiết
Cho nửa đường tròn tâm O, đường kính AB 2R. Trên tia đối của tia AB lấy điểm E (khác với điểm A). Tiếp tuyến kẻ từ điểm E cắt các tiếp tuyến kẻ từ điểm A và B của nửa đường tròn (O) lần lượt tại C và D. Gọi M là tiếp điểm của tiếp tuyến kẻ từ điểm E. Tìm khẳng định sai A. Tứ giác OACM là tứ giác nội tiếp. B. Tứ giác OBDM là tứ giác nội tiếp C. Tứ giác ACDB là hình thang vuông D. Tứ giác ACDO là tứ giác nội tiếp
Đọc tiếp
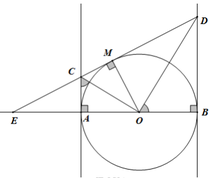
Cho nửa đường tròn tâm O, đường kính AB = 2R. Trên tia đối của tia AB lấy điểm E (khác với điểm A). Tiếp tuyến kẻ từ điểm E cắt các tiếp tuyến kẻ từ điểm A và B của nửa đường tròn (O) lần lượt tại C và D. Gọi M là tiếp điểm của tiếp tuyến kẻ từ điểm E. Tìm khẳng định sai
A. Tứ giác OACM là tứ giác nội tiếp.
B. Tứ giác OBDM là tứ giác nội tiếp
C. Tứ giác ACDB là hình thang vuông
D. Tứ giác ACDO là tứ giác nội tiếp
Chọn đáp án D.
Suy ra OMDB là tứ giác nội tiếp.
Đúng 0
Bình luận (0)
Cho (O) và 1 điểm A nằm ngoài đường tròn. Từ A kẻ 2 tiếp tuyến AB, AC (B và C là 2 tiếp điểm). Từ A kẻ thêm các tuyến AMN đi qua (O) và nằm trong góc BAO. Chúng minh AB.AB=AM.AN
Xét ΔABM và ΔANB có
góc ABM=góc ANB
góc BAM chung
=>ΔABM đồng dạng với ΔANB
=>AB/AN=AM/AB
=>AB^2=AN*AM
Đúng 3
Bình luận (0)
Cho nửa đường tròn tâm (O,R) đường kính AB. Trên tia đối của BA lấy G, từ G, A, B vẽ các tiếp tuyến với đường tròn (O). Tiếp tuyến tại G cắt 2 tiếp tuyến kẻ từ A và B tại C và D. Gọi N là tiếp điểm của tiếp tuyến kẻ từ G CMR: a) Tứ giác BDND nội tiếp b) CN/CGON/DG và tích ACBD ko phụ thuộc vào vị trí điểm G trên tia đối BACâu (a) có vẻ như là sai đề hay sao ý ạ phiền các anh/chị sửa lại giúp em với, em cảm ơn nhiều ^^
Đọc tiếp
Cho nửa đường tròn tâm (O,R) đường kính AB. Trên tia đối của BA lấy G, từ G, A, B vẽ các tiếp tuyến với đường tròn (O). Tiếp tuyến tại G cắt 2 tiếp tuyến kẻ từ A và B tại C và D. Gọi N là tiếp điểm của tiếp tuyến kẻ từ G
CMR: a) Tứ giác BDND nội tiếp
b) CN/CG=ON/DG và tích AC>BD ko phụ thuộc vào vị trí điểm G trên tia đối BA
"Câu (a) có vẻ như là sai đề hay sao ý ạ phiền các anh/chị sửa lại giúp em với, em cảm ơn nhiều ^^"
Cho nửa đường tròn tâm (O,R) đường kính AB. Trên tia đối của BA lấy G, từ G, A, B vẽ các tiếp tuyến với đường tròn (O). Tiếp tuyến tại G cắt 2 tiếp tuyến kẻ từ A và B tại C và D. Gọi N là tiếp điểm của tiếp tuyến kẻ từ G CMR: a) Tứ giác BDND nội tiếp b) CN/CGON/DG và tích ACBD ko phụ thuộc vào vị trí điểm G trên tia đối BACâu (a) có vẻ như là sai đề hay sao ý ạ phiền các anh/chị sửa lại giúp em với, em cảm ơn nhiều ^^
Đọc tiếp
Cho nửa đường tròn tâm (O,R) đường kính AB. Trên tia đối của BA lấy G, từ G, A, B vẽ các tiếp tuyến với đường tròn (O). Tiếp tuyến tại G cắt 2 tiếp tuyến kẻ từ A và B tại C và D. Gọi N là tiếp điểm của tiếp tuyến kẻ từ G
CMR: a) Tứ giác BDND nội tiếp
b) CN/CG=ON/DG và tích AC>BD ko phụ thuộc vào vị trí điểm G trên tia đối BA
"Câu (a) có vẻ như là sai đề hay sao ý ạ phiền các anh/chị sửa lại giúp em với, em cảm ơn nhiều ^^"
Từ điểm A nằm ngoài đường tròn (O),kẻ tiếp tuyến AM với đường tròn(M là tiếp điểm). Kẻ dây MN vuông góc với AO tại H. Kẻ cát tuyến ABC với đường tròn( điểm B nằm giữa A và C). a)CM: AN là tiếp tiếp tuyến. b)Tiếp tuyến tại B và C của đường tròn (O) cắt nhau tại K, gọi I là trung điểm của BC. CM:OI.OK=ON.ON(ON bình) và 3 điểm K,H,N thẳng hàng
a: Ta có: ΔOMN cân tại O
mà OA là đường cao
nên OA là phân giác củagóc MON
Xét ΔOMA và ΔONA có
OM=ON
góc MOA=góc NOA
OA chung
Do đó: ΔOMA=ΔONA
=>góc ONA=90 độ
=>AN là tiếp tuyến của (O)
b: Xét (O) có
KC,KB là tiếp tuyến
nên KC=KB
=>K năm trên trung trực của BC(1)
ΔOBC cân tại O
mà OI là trung tuyến
nên OI là trung trực của BC(2)
Từ (1), (2) suy ra O,I,K thẳng hàng
=>OK vuông góc với BC tại I
=>OI*OK=OB^2=ON^2
Đúng 0
Bình luận (0)
Cho (O) đường kính AB . Trên tia đối của tia AB lấy điểm E . Từ E ,A,B kẻ tiếp tuyến với nửa đường tròn . Tiếp tuyến kẻ từ E cắt 2 tiếp tuyến A và B lần lượt tại C và D
a, Gọi M là tiếp điểm của tiếp tuyến kẻ từ E đến nửa đường tròn . CM : ACMO nội tiếp
b, DM.CE = CM.DE
c, gọi N là giao điểm của AD và BD . CM : MN//BD
a/
Ta có M và A cùng nhìn OC dưới 1 góc \(90^o\) => ACMO là tứ giác nội tiếp
b/
Xét tg vuông BED và tg vuông AEC có \(\widehat{BED}\) chung
=> tg BED đồng dạng với tg AEC (g.g.g)
\(\Rightarrow\dfrac{DB}{CA}=\dfrac{DE}{CE}\)
Mà
\(DB=DM;CA=CM\) (Hai tiếp tuyến cùng xp từ 1 điểm...)\(\Rightarrow\dfrac{DB}{CA}=\dfrac{DM}{CM}=\dfrac{DE}{CE}\Rightarrow DM.CE=CM.DE\)
c/
Ta có
\(CA\perp AB\left(gt\right);DB\perp AB\left(gt\right)\) => CA//DB
\(\Rightarrow\dfrac{BN}{CN}=\dfrac{DB}{CA}\) (Talet)
Mà \(\dfrac{DM}{CM}=\dfrac{DB}{CA}\left(cmt\right)\)
\(\Rightarrow\dfrac{BN}{CN}=\dfrac{DM}{CM}\) => MN//BD (Talet đảo trong tam giác)
Đúng 0
Bình luận (0)
Từ điểm A nằm ngoài đường tròn (O; R), kẻ 2 tiếp tuyến AB, AC đến đường tròn(O) (B, C là 2 tiếp điểm). Gọi H là giao điểm của OA và BCTừ điểm A nằm ngoài đường tròn (O; R), kẻ 2 tiếp tuyến AB, AC đến đường tròn(O) (B, C là 2 tiếp điểm). Gọi H là giao điểm của OA và BC.a) Chứng minh: OA là đường trung trực của BC và OH.OA R2b) Đoạn thẳng OA cắt đường tròn (O) tại M. Chứng minh: BM là tia phân giác củagóc ABH.c) Trên đoạn AH lấy điểm D sao cho HB HD, qua D kẻ DE vuông góc OA (E thuộcAB), gọi I l...
Đọc tiếp
Từ điểm A nằm ngoài đường tròn (O; R), kẻ 2 tiếp tuyến AB, AC đến đường tròn(O) (B, C là 2 tiếp điểm). Gọi H là giao điểm của OA và BCTừ điểm A nằm ngoài đường tròn (O; R), kẻ 2 tiếp tuyến AB, AC đến đường tròn
(O) (B, C là 2 tiếp điểm). Gọi H là giao điểm của OA và BC.
a) Chứng minh: OA là đường trung trực của BC và OH.OA = R2
b) Đoạn thẳng OA cắt đường tròn (O) tại M. Chứng minh: BM là tia phân giác của
góc ABH.
c) Trên đoạn AH lấy điểm D sao cho HB = HD, qua D kẻ DE vuông góc OA (E thuộc
AB), gọi I là trung điểm của OE. Tính số đo góc BHI và độ dài cạnh BE theo R?
.........Giúp mình với ạ...........
(O) (B, C là 2 tiếp điểm). Gọi H là giao điểm của OA và BC.
a) Chứng minh: OA là đường trung trực của BC và OH.OA = R2
b) Đoạn thẳng OA cắt đường tròn (O) tại M. Chứng minh: BM là tia phân giác của
góc ABH.
c) Trên đoạn AH lấy điểm D sao cho HB = HD, qua D kẻ DE vuông góc OA (E thuộc
AB), gọi I là trung điểm của OE. Tính số đo góc BHI và độ dài cạnh BE theo R?
.........Giúp mình với ạ...........
a Xét (O) có
AB,AC là tiếp tuyến
nên AB=AC
mà OB=OC
nên OA là trung trực của BC
=>OA vuông góc với BC
=>OH*OA=OB^2=R^2
b: góc ABM=góc ACM
góc HBM=90 độ-góc OMB=90 độ-góc OBM=góc ABM
=>BM là phân giác của góc ABH
Đúng 0
Bình luận (0)
từ điểm A ngoài đường tròn (O),kẻ tiếp tuyến AB( B là tiếp điểm ) và cát tuyến AMN với đường tròn (O) sao cho tia AO nằm giữa hai điểm AB và AM , từ O kẻ OL vuông góc với MN ( L thuộc MN) chứng minh:
a tứ giác ABOL nội tiếp
b AB^2=AM.AN
a: ΔOMN cân tại O có OL là đường cao
nên L là trung điểm của MN
góc ABO=góc OLA=90 độ
=>ABLO nội tiếp
b: Xét ΔABM và ΔANB có
góc ABM=góc ANB
góc BAM chung
=>ΔABM đồng dạng với ΔANB
=>AB/AN=AM/AB
=>AB^2=AN*AM
Đúng 0
Bình luận (0)
(2 điểm) Từ 1 điểm A ở ngoài đường tròn (O), kẻ tiếp tuyến AB với đường tròn (O)
( B là tiếp điểm). Gọi I là trung điểm của đoạn thẳng AB, kẻ tiếp tuyến IM với đường tròn (O) ( M là tiếp điểm).
a)Chứng minh IA = IM.
b)Chứng minh Tam giác ABM là tam giác vuông tại M.
c)Vẽ đường kính BC của đường tròn (O). Chứng minh 3 điểm A, M, C thẳng hàng.
a: Xét (O) có
IM là tiếp tuyến
IB là tiếp tuyến
Do đó: IM=IB
mà IA=BI
nên IA=IM
b: Xét ΔABM có
MI là đường trung tuyến
MI=AB/2
Do đó: ΔMAB vuông tại M
c: Xét (O) có
ΔBMC nội tiếp
BC là đường kính
Do đó: ΔBMC vuông tại M
hay BM⊥CM
mà BM⊥AM
và CM,AM có điểm chung là M
nên A,M,C thẳng hàng
Đúng 1
Bình luận (0)