Trong mặt phẳng Ox, cho hình bình hành 0ABC, A(1;2). Điểm B nằm trên đường thẳng d: x+y-4=0
Hỏi điểm C nằm trên đường thẳng nào.
Những câu hỏi liên quan
1.Trong mặt phẳng tọa độ Oxy cho hình bình hành ABCD với A (- 6;1); B (2;2) C (1;5) tọa độ đỉnh D là:
A. (5;2)
B. (-7;4)
C. (5;4)
D. (7;-4)
2.Trong mặt phẳng tọa độ Oxy cho tam giác ABC với A (- 1;3); B (2;1) C (5;5) tọa độ đỉnh D là của hình bình hành ABCD:
A. (0;4)
B. (8;1)
C. (8;3)
D. (-8;3)
Hướng dẫn em cách làm với ạ. Em cảm ơn nhiều.
1, Gọi tọa độ điểm D(x;y)
Ta có:\(\overrightarrow{AB}\left(8;1\right)\)
\(\overrightarrow{DC}\left(1-x;5-y\right)\)
Tứ giác ABCD là hình bình hành khi
\(\overrightarrow{AB}=\overrightarrow{DC}\)
\(\Leftrightarrow1-x=8;5-y=1\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-7\\y=4\end{matrix}\right.\)
Vậy tọa độ điểm D(-7;4)
Đúng 1
Bình luận (1)
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Trong mặt phẳng (ABCD) vẽ
đường thẳng d đi qua A và không song song với các cạnh của hình bình hành. Trên cạnh SC lấy
điểm M. Tìm thiết diện của hình chóp khi cắt bởi mặt phẳng (M,d)
Trong mặt phẳng tọa độ Oxy cho A(3; -1) ; B( -1; 2) và I( 1; -1) . Xác định tọa độ các điểm C; D sao cho tứ giác ABCD là hình bình hành biết I là trọng tâm tam giác ABC. Tìm tọa tâm O của hình bình hành ABCD A. B. C. D.
Đọc tiếp
Trong mặt phẳng tọa độ Oxy cho A(3; -1) ; B( -1; 2) và I( 1; -1) . Xác định tọa độ các điểm C; D sao cho tứ giác ABCD là hình bình hành biết I là trọng tâm tam giác ABC. Tìm tọa tâm O của hình bình hành ABCD
A. 
B. 
C. 
D. 
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Trong mặt phẳng đáy vẽ đường thẳng d đi qua A và không song song với các cạnh hình bình hành, d cắt đoạn BC tại E. Gọi C' là một điểm nằm trên cạnh SC.
a) Tìm giao điểm M của CD và mặt phẳng (C'AE)
b) Tìm thiết diện của hình chóp cắt bởi mặt phẳng (C'AE)
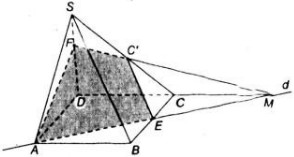
a) Trong (ABCD) gọi M = AE ∩ DC => M ∈ AE, AE ⊂ ( C'AE) => M ∈ ( C'AE). Mà M ∈ CD => M = DC ∩ (C'AE).
b)
Do M = DC ∩ (C'AE) nên M ∈ (SDC),.
Trong (SDC) : MC' ∩ SD = F.
Ta có:
\(\left(C'AE\right)\cap\left(SDC\right)=FC'\)
\(\left(C'AE\right)\cap\left(SAD\right)=AF\)
\(\left(C'AE\right)\cap\left(ABCD\right)=AE\)
\(\left(C'AE\right)\cap\left(SBC\right)=C'E\)
Vậy thiết diện là AEC'F.
Đúng 0
Bình luận (0)
Giải mục 1 trang 114, 115, 116, 117 SGK Toán 11 tập 1 - Cánh Diều
14 tháng 7 2023 lúc 21:00
Cho mặt phẳng (P), hình bình hành ABCD và đường thẳng l cắt mặt phẳng (P). Xác định hình chiếu song song của hình bình hành ABCD trên mặt phẳng (P) theo phương l biết rằng mặt phẳng (ABCD) không song song với l.
Nhìn hình vẽ ta thấy: A'B'C'D' là hình chiếu song song của hình bình hành ABCD trên mặt phẳng (P) theo phương l.
Đúng 0
Bình luận (0)
Trên mặt phẳng (α) cho hình bình hành
A
1
B
1
C
1
D
1
. Về một phía đối với mặt phẳng (α) ta dựng hình bình hành
A
2
B
2
C
2
D
2
. Trên các đoạn
A
1
A...
Đọc tiếp
Trên mặt phẳng (α) cho hình bình hành A 1 B 1 C 1 D 1 . Về một phía đối với mặt phẳng (α) ta dựng hình bình hành A 2 B 2 C 2 D 2 . Trên các đoạn A 1 A 2 , B 1 B 2 , C 1 C 2 , D 1 D 2 ta lần lượt lấy các điểm A, B, C, D sao cho
A A 1 A A 2 = B B 1 B B 2 = C C 1 C C 2 = D D 1 D D 2 = 3
Chứng minh rằng tứ giác ABCD là hình bình hành
Trong mặt phẳng Oxy, cho A( -2; 0) ; B( 5; -4) ; C( -5; 1). Tọa độ điểm D để tứ giác ABCD là hình bình hành là:
A. D( -8; 5).
B. D( 5; 8).
C. D( 8; 5).
D. D( 8; -5).
Chọn D.
Ta có: tứ giác ABCD là hình bình hành khi
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy, cho A( -2; 0) ; B( 5; -4) ; C( -5; 1). Tọa độ điểm D để tứ giác ABCD là hình bình hành là:
A.D( -8; 5)
B. D( 5; 8)
C.D( 8; 5)
D.D( 8; -5) .
Ta có: tứ giác ABCD là hình bình hành khi
Đúng 0
Bình luận (0)
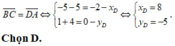
Trong mặt phẳng oxy cho 3 điểm A(-5;2) B(4:-3) C(6:1) tìm tọa độ D để tứ giác abcd là hình bình hành
Gọi \(D\left(x;y\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(9;-5\right)\\\overrightarrow{CD}=\left(6-x;1-y\right)\end{matrix}\right.\)
ABCD là hình bình hành khi \(\overrightarrow{AB}=\overrightarrow{DC}\)
\(\Rightarrow\left\{{}\begin{matrix}6-x=9\\1-y=-5\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=-3\\y=6\end{matrix}\right.\)
\(\Rightarrow D\left(-3;6\right)\)
Đúng 0
Bình luận (0)