Trong mặt phẳng tọa độ Oxy phép vị tự tâm I(1;2) tỉ số k = 5, biến điểm M(2;-3) thành điểm M’ có tọa độ:
A. M'(1;-5)
B.M'(8;13)
C. M'(6;-23)
D.M'(6;-27)
Phép vị tự tâm I(1; 2) tỉ số k = 5 biến điểm M(2; -3) thành điểm M’(x; y)
⇔ I M ' → = 5 I M → ⇔ x − 1 = 5 2 − 1 y − 2 = 5 − 3 − 2 ⇔ x = 6 y = − 23
Suy ra M’(6; -23).
Đáp án C
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy phép vị tự tâm I(0;2) tỉ số k = -1/2 , biến điểm M(12;-3) thành điểm M’ có tọa độ:
A. M'(12;-1/2)
B. M'(-6;9/2)
C. M'(6;-2)
D. M'(-6;12)
I M ' → = − 1 2 I M → ⇔ x − 0 = − 1 2 . ( 12 − 0 ) = − 6 y − 2 = − 1 2 ( − 3 − 2 ) = 5 2 ⇒ x = − 6 y = 9 2
Đáp án B
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có tâm I(0;−1) , bán kính R 2. Ảnh của (C) qua việc thực hiện liên tiếp phép quay tâm O góc quay 180
°
và phép vị tự tâm O tỉ số 2 A.
(
x
−
2
)
2
+
y
2
16
B.
x
2
+
y...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có tâm I(0;−1) , bán kính R = 2. Ảnh của (C) qua việc thực hiện liên tiếp phép quay tâm O góc quay 180 ° và phép vị tự tâm O tỉ số 2
A. ( x − 2 ) 2 + y 2 = 16
B. x 2 + y − 2 2 = 4
C. ( x − 2 ) 2 + y 2 = 4
D. x 2 + y − 2 2 = 16
Đáp án D
Q ( O ; 180 o ) : I → I ' (0;1) , bán kính 2
I ' ' = V O ; k ( I ' ) -> I”(0;2), bán kính 4
Phương trình đường tròn (C”): x 2 + y − 2 2 = 16
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy phép vị tự tâm I(1;4) tỉ số k = -2, biến đường thẳng d có phương trình : 7x + 3y - 4 = 0 thành đường thẳng d’ có phương trình:
A. 7x + 3y - 49 = 0
B. 3x + 7y - 47 = 0
C. 7x + 3y + 49 = 0
D. 3x + 7y - 49 = 0
Phép vị tự tâm I (1; 4) tỉ số k = -2, biến M(x; y) thuộc d thành M’(x’;y’) thuộc d;
⇒ I M ' → = - 2 I M →
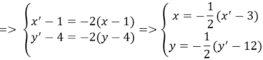
Thay vào phương trình d ta được
7. − 1 2 ( x ' − 3 ) + 3. − 1 2 ( y ' − 12 ) − 4 = 0 ⇔ 7 ( x ' − 3 ) + 3 ( y ' − 12 ) + 8 = 0 ⇔ 7 x ' + 3 y ' − 49 = 0
⇒ d' có phương trình là: 7x + 3y - 49 = 0.
Đáp án A
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho (d): x + 4y – 3 0 và điểm A(–1;1). Ảnh của (d) qua phép vị tự tâm A tỉ số 3 A.
x
−
4
y
+
3
0
B.
−
x
+
4
y
−
3
0
C.
−
x
−
4
y
+
3
0
D. Kết quả khác
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho (d): x + 4y – 3 = 0 và điểm A(–1;1). Ảnh của (d) qua phép vị tự tâm A tỉ số 3
A. x − 4 y + 3 = 0
B. − x + 4 y − 3 = 0
C. − x − 4 y + 3 = 0
D. Kết quả khác
Đáp án C
Ta có: A ∈ (d) => Phép vị tự tâm A tỉ số 3 biến d thành chính nó
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có tâm I(0;−1) , bán kính R 3. Ảnh của (C) qua việc thực hiện liên tiếp phép quay tâm O góc quay 180
°
và phép vị tự tâm O tỉ số 2, phép tịnh tiến theo vectơ
u
→
1
;
2
A.
x
−
4
2
+
y...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có tâm I(0;−1) , bán kính R = 3. Ảnh của (C) qua việc thực hiện liên tiếp phép quay tâm O góc quay 180 ° và phép vị tự tâm O tỉ số 2, phép tịnh tiến theo vectơ u → 1 ; 2
A. x − 4 2 + y − 1 2 = 9
B. x − 1 2 + y − 4 2 = 9
C. x − 1 2 + y − 4 2 = 36
D. x − 4 2 + y − 1 2 = 36
Đáp án C
Q ( O ; 180 o ) : I → I ' (0;1) , bán kính 3
I ' ' = V O ; k ( I ' ) => I”(0;2), bán kính 6
T u → ( I " ) = I ' " 1 ; 4 , bán kính 6
Phương trình đường tròn (C”): ( x − 1 ) 2 + y − 4 2 = 36
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy phép vị tự tâm O(0;0) tỉ số k = -3, biến điểm M(-4;3) thành điểm M’ có tọa độ
A. M'(-12;-9)
B. M'(12;9)
C. M'(-9;12)
D. M'(12;-9)
O M ' → = - 3 O M →
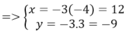
⇒ M'(12; -9)
Đáp án D
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy cho đường tròn tâm I(2;-2), bán kính R 4. Viết phương trình đường tròn là ảnh của đường tròn (I;R) qua phép vị tự tâm O, tỉ số
1
2
. A.
x
-
4
2
+
(
y
+
4
)
2
4
B. ...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy cho đường tròn tâm I(2;-2), bán kính R = 4. Viết phương trình đường tròn là ảnh của đường tròn (I;R) qua phép vị tự tâm O, tỉ số 1 2 .
A. x - 4 2 + ( y + 4 ) 2 = 4
B. x - 4 2 + ( y + 4 ) 2 = 64
C. x - 1 2 + ( y + 1 ) 2 = 4
D. x - 1 2 + ( y + 1 ) 2 = 64
Trong mặt phẳng tọa độ Oxy phép vị tự tâm O(0;0) tỉ số k = -5, biến đường thẳng d có phương trình : 2x + 3y - 4 = 0 thành đường thẳng d’ có phương trình:
A. 2x + 3y - 16 = 0
B. 3x + 2y - 4 = 0
C. 3x + 2y - 20 = 0
D. 2x + 3y + 20 = 0
Phép vị tự tâm O(0; 0) tỉ số k = -5, biến M(x; y) thuộc d thành M’(x’, y’) thuộc d’ ⇒ O M ' → = - 5 O M →
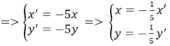
Thay vào phương trình d ta được:
2 . − 1 5 x ' + 3. − 1 5 y ' − 4 = 0 ⇔ − 2 5 x ' + − 3 5 y ' − 4 = 0 ⇔ 2 x ' + 3 y ' + 20 = 0
⇒ phương trình của d’ là 2x + 3y + 20 = 0
Đáp án D
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho đường tròn
C
:
x
2
+
y
2
+
2
x
-
4
y
+
1
0
. Ảnh của đường tròn (C) qua phép vị tự tâm O tỷ sốk 2 có phương trình là A.
x
2
+
y
2
+
4
x
-
8
y...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho đường tròn C : x 2 + y 2 + 2 x - 4 y + 1 = 0 . Ảnh của đường tròn (C) qua phép vị tự tâm O tỷ số
k = 2 có phương trình là
A. x 2 + y 2 + 4 x - 8 y + 4 = 0
B. x 2 + y 2 - 4 x + 8 y + 4 = 0
C. x 2 + y 2 + 4 x - 8 y - 4 = 0
D. x 2 + y 2 + 4 x - 8 y + 2 = 0
