Trong không gian với hệ tọa độ Oxyz, gọi a,b,c lần lượt là khoảng cách từ điểm M(1;3;2) đến ba mặt phẳng tọa độ (Oxy), (Oyz), (Oxz). Tính P = a + b 2 + c 3
A. 12
B. 32
C. 30
D. 18
Trong không gian với hệ tọa độ Oxyz, gọi a,b,c lần lượt là khoảng cách từ điểm M(1;3;2) đến ba mặt phẳng tọa độ (Oxy), (Oyz), (Oxz). Tính P = a + b 2 + c 3
A. 12
B. 32
C. 30
D. 18
Trong không gian với hệ tọa độ Oxyz, gọi a,b,c lần lượt là khoảng cách từ điểm M 1 ; 3 ; 2 đến ba mặt phẳng tọa độ O x y , O y z , O x z . Tính P = a + b 2 + c 3
A. P = 12.
B. P = 32.
C. P = 30.
D. P = 18.
Đáp án C
Áp dụng STUDY TIPS bên, ta có:
Khoảng cách từ điểm M đến mặt phẳng O x y là a=2.
Khoảng cách từ điểm M đến mặt phẳng O x y là b=1.
Khoảng cách từ điểm M đến mặt phẳng O x y là c=3 .
Vậy P = a + b 2 + c 3 = 2 + 1 2 + 3 3 = 30 .
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng ( P ) : m x + ( m + 1 ) y − z − 2 m − 1 = 0 , với m là tham số. Gọi (T) là tập hợp các điểm H m là hình chiếu vuông góc của điểm H ( 3 ; 3 ; 0 ) trên (P). Gọi a, b lần lượt là khoảng cách lớn nhất, khoảng cách nhỏ nhất từ O đến một điểm thuộc (T). Khi đó, a + b bằng
A. 5 2 .
B. 3 3 .
C. 8 2 .
D. 4 2 .
Trong không gian với hệ trục tọa độ Oxyz, cho điểm M thỏa mãn OM = 7. Biết rằng khoảng cách từ M đến (Oxz), (Oyz) lần lượt là 2 và 3. Tính khoảng cách từ M đến (Oxy).
A. 12
B. 5
C. 2
D. 6
Đáp án D
Gọi M ( a ; b ; c ) ⇒ d M , O x z = b = 2 ; d M , O y z = a = 3
Do O M = 7 ⇒ a 2 + b 2 + c 2 = 49 ⇒ c = 49 - a 2 - b 2 = 6
Vậy d M ; O x y = 6 .
Trong không gian với hệ tọa độ Oxyz, cho điểm M(4;1;9). Gọi (P) là mặt phẳng đi qua M và cắt 3 tia Ox, Oy, Oz lần lượt tại các điểm A,B,C (khác 0) sao cho (OA+OB+OC) đạt giá trị nhỏ nhất. Tính khoảng cách d từ điểm I(0;1;3) đến mặt phẳng (P).
A. d= 34 5
B. d= 36 5
C. d= 24 7
D. d= 30 7
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) cắt ba trục tọa độ lần lượt là A(a;0;0), B(0;b;0), C(0;0;c) với a b c ≠ 0 thỏa mãn 2 a + b = a b 2 c + 1 - 1 b . Khoảng cách lớn nhất từ O đến mặt phẳng (P) là:
A. 7
B. 17
C. 3
D. 1 17
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(-1;3;4), B(3;1;0). Gọi M là điểm trên mặt phẳng (Oxz) sao cho tổng khoảng cách từ M đến A và B là ngắn nhất. Tìm hoành độ x 0 của điểm M.
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, Cho bốn điểm A(2;0;0), B(0;2;0), C(0;0;2) và D(2;2;2) Gọi M, N lần lượt là trung điểm của (S) và AB. Tọa độ trung điểm I của MN là:
A. I(1;-1;2)
B. I(1;1;0)
C. I 1 2 ; 1 2 ; 1
D. I(1;1;1)
Đáp án D
Áp dụng công thức trung điểm ta có

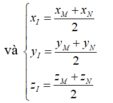
Suy ra
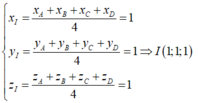
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A - 2 ; 1 ; 0 , B 4 ; 4 ; - 3 , C 2 ; 3 ; - 2 và đường thẳng d : x - 1 1 = y - 1 - 2 = z - 1 - 1 . Gọi α là mặt phẳng chứa d sao cho A, B, C ở cùng phía đối với mặt phẳng α . Gọi d 1 , d 2 , d 3 lần lượt là khoảng cách từ A, B, C đến α . Tìm giá trị lớn nhất của T = d 1 + 2 d 2 + 3 d 3 .
A. T m a x = 2 21
B. T m a x = 6 14
C. T m a x = 14 + 203 3 + 3 21
D. T m a x = 203