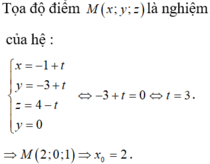Các câu hỏi tương tự
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A (1;2;3), B (0;4;5). Gọi M là điểm sao cho MA2MB. Khoảng cách từ điểm M đến mặt phẳng (P): 2x-2y-z+60 đạt giá trị nhỏ nhất xấp xỉ là bao nhiêu? A.1,72 B.1,47 C.1,64 D.1,59
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A (1;2;3), B (0;4;5). Gọi M là điểm sao cho MA=2MB. Khoảng cách từ điểm M đến mặt phẳng (P): 2x-2y-z+6=0 đạt giá trị nhỏ nhất xấp xỉ là bao nhiêu?
A.1,72
B.1,47
C.1,64
D.1,59
Trong không gian với hệ tọa độ Oxyz, cho điểm A(2;1;3) và mặt phẳng
P
:
x
+
m
y
+
(
2
m
+
1
)
z
-
(
2
+
m
)
0
với m là tham số. Gọi điểm H(a;b;c) là hình chiếu vuông góc của điểm A trên (P). Tính a+b khi khoảng cách từ điểm A đến (P) lớn n...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm A(2;1;3) và mặt phẳng P : x + m y + ( 2 m + 1 ) z - ( 2 + m ) = 0 với m là tham số. Gọi điểm H(a;b;c) là hình chiếu vuông góc của điểm A trên (P). Tính a+b khi khoảng cách từ điểm A đến (P) lớn nhất.
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, gọi a,b,c lần lượt là khoảng cách từ điểm M(1;3;2) đến ba mặt phẳng tọa độ (Oxy), (Oyz), (Oxz). Tính P = a + b 2 + c 3
A. 12
B. 32
C. 30
D. 18
Trong không gian với hệ tọa độ Oxyz, gọi a,b,c lần lượt là khoảng cách từ điểm M(1;3;2) đến ba mặt phẳng tọa độ (Oxy), (Oyz), (Oxz). Tính P = a + b 2 + c 3
A. 12
B. 32
C. 30
D. 18
Trong không gian với hệ tọa độ Oxyz cho điểm A(2;1;3) và mặt phẳng (P): x + my + (2m + 1) - m - 2 = 0. Gọi H (a;b;c) là hình chiếu vuông góc của điểm A trên (P) Khi khoảng cách từ điểm A đến (P) lớn nhất, tính a + b
A. 2
B. 1
C. 3 2
D. 0
Trong không gian với hệ tọa độ Oxyz cho điểm A (2; 1; 3) và mặt phẳng (P): x + my + (2m + 1)z – m – 2 0, m là tham số. Gọi H (a; b; c) là hình chiếu vuông góc của điểm A trên (P). Tính a + b khi khoảng cách từ điểm A đến (P) lớn nhất? A. a + b -1/2 B. a + b 2 C. a + b 0 D. a + b 3/2
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho điểm A (2; 1; 3) và mặt phẳng (P): x + my + (2m + 1)z – m – 2 = 0, m là tham số. Gọi H (a; b; c) là hình chiếu vuông góc của điểm A trên (P). Tính a + b khi khoảng cách từ điểm A đến (P) lớn nhất?
A. a + b = -1/2
B. a + b = 2
C. a + b = 0
D. a + b = 3/2
Trong không gian với hệ tọa độ Oxyz, cho điểm M(4;1;9). Gọi (P) là mặt phẳng đi qua M và cắt 3 tia Ox, Oy, Oz lần lượt tại các điểm A,B,C (khác 0) sao cho (OA+OB+OC) đạt giá trị nhỏ nhất. Tính khoảng cách d từ điểm I(0;1;3) đến mặt phẳng (P). A. d
34
5
B. d
36
5
C. d
24
7
D. d
30
7
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm M(4;1;9). Gọi (P) là mặt phẳng đi qua M và cắt 3 tia Ox, Oy, Oz lần lượt tại các điểm A,B,C (khác 0) sao cho (OA+OB+OC) đạt giá trị nhỏ nhất. Tính khoảng cách d từ điểm I(0;1;3) đến mặt phẳng (P).
A. d= 34 5
B. d= 36 5
C. d= 24 7
D. d= 30 7
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A (-1; 2; 4) và B (0; 1; 5). Gọi (P) là mặt phẳng đi qua A sao cho khoảng cách từ B đến (P) là lớn nhất. Khi đó, khoảng cách d từ O đến mặt phẳng (P) bằng bao nhiêu?
A
.
d
-
3
3
B
.
d
3
C
.
d
1...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A (-1; 2; 4) và B (0; 1; 5). Gọi (P) là mặt phẳng đi qua A sao cho khoảng cách từ B đến (P) là lớn nhất. Khi đó, khoảng cách d từ O đến mặt phẳng (P) bằng bao nhiêu?
A . d = - 3 3
B . d = 3
C . d = 1 3
D . d = 1 3
Trong không gian với hệ tọa độ Oxyz, cho hai điểm M(0;-1;2) và N(-1;1;3). Một mặt phẳng (P) đi qua M, N sao cho khoảng cách từ điểm K(0;0;2) đến mặt phẳng (P) đạt giá trị lớn nhất. Tìm tọa độ véctơ pháp tuyến
n
→
của mặt phẳng A.
n
→
(1;-1;1) B.
n
→
(1;1;-1) C. ...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai điểm M(0;-1;2) và N(-1;1;3). Một mặt phẳng (P) đi qua M, N sao cho khoảng cách từ điểm K(0;0;2) đến mặt phẳng (P) đạt giá trị lớn nhất. Tìm tọa độ véctơ pháp tuyến n → của mặt phẳng
A. n → =(1;-1;1)
B. n → =(1;1;-1)
C. n → =(2;-1;1)
D. n → =(2;1;-1)