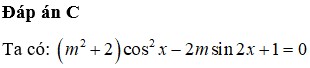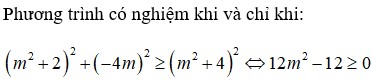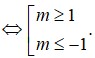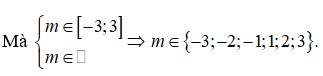Có tất cả bao nhiêu giá trị nguyên dương của tham số m thuộc [-10 ; 10] để pt \(\left(m^2-9\right)x=3m\left(m-3\right)\) có nghiệm duy nhất

Những câu hỏi liên quan
Có tất cả bao nhiêu giá trị nguyên dương của tham số m để phương trình
4
1
+
x
+
4
1
-
x
6
-
m
2
2
+
x
-...
Đọc tiếp
Có tất cả bao nhiêu giá trị nguyên dương của tham số m để phương trình 4 1 + x + 4 1 - x = 6 - m 2 2 + x - 2 2 - x có nghiệm thuộc đoạn 0 ; 1 ?
A. 4
B. 3
C. 1
D. 2
Có tất cả bao nhiêu giá trị nguyên không dương của tham số m để phương trình 2 x + m = x − 1 có nghiệm duy nhất?
A. 4
B. 3
C. 1
D. 2
⇔ x − 1 ≥ 0 2 x + m = x − 1 2 ⇔ x ≥ 1 x 2 − 4 x + 1 − m = 0 ( * )
Phương trình có nghiệm duy nhất khi hệ có nghiệm duy nhất.
![]()
TH1: ∆ ' = 0 ⇔ m = - 3 thì (*) có nghiệm kép x = 2 ≥ 1 (thỏa).
TH2: ∆ ' > 0 ⇔ m > - 3 thì phương trình có nghiệm duy nhất khi (*) có 2 nghiệm thỏa mãn:
x 1 < 1 < x 2 ⇔ x 1 - 1 x 2 - 1 < 0 ⇔ x 1 x 2 - x 1 + x 2 + < 0
⇔ 1 - m - 4 + < 0 ⇔ m > - 2
Do m không dương nên m ∈ {−1; 0}
Kết hợp với trường hợp m = −3 ở trên ta được 3 giá trị của m thỏa mãn bài toán.
Đáp án cần chọn là: B
Đúng 0
Bình luận (0)
Có tất cả bao nhiêu giá trị nguyên dương của tham số m để hàm số
y
m
x
4
-
m
-
5
x
2
-
3
đồng biến trên khoảng (0;+¥). A. 6 B. 4 C. 3 D. 5
Đọc tiếp
Có tất cả bao nhiêu giá trị nguyên dương của tham số m để hàm số y = m x 4 - m - 5 x 2 - 3 đồng biến trên khoảng (0;+¥).
A. 6
B. 4
C. 3
D. 5
Có tất cả bao nhiêu giá trị nguyên dương của tham số thực m để phương trình
x
2
+
4
m
x
2
+
1
2
m
-
3
m
2
có nghiệm trên [0;2] A. 1 B. 2 C. 4 D. 0
Đọc tiếp
Có tất cả bao nhiêu giá trị nguyên dương của tham số thực m để phương trình x 2 + 4 m x 2 + 1 = 2 m - 3 m 2 có nghiệm trên [0;2]
A. 1
B. 2
C. 4
D. 0
Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số y=|3x⁴-mx³+6x²+m-3| đồng biến trên khoảng (0- dương vô cùng)
Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình x4-2x2+3-2m=0 có nghiệm thuộc (-2;2) ?
- Đặt \(a=x^2\left(a\ge0\right)\)
PTTT \(a^2-2a-2m+3=0\)
Có : \(\Delta^,=\left(-1\right)^2-\left(-2m+3\right)=1+2m-3=2m-2\)
- Theo viet : \(\left\{{}\begin{matrix}a_1+a_2=2\\a_1a_2=3-2m\end{matrix}\right.\)
- Để phương trình đề có nghiệm :
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta^,\ge0\\a_1+a_2>0\\a_1a_2\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2m-2\ge0\\3-2m\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ge1\\m\le\dfrac{3}{2}\end{matrix}\right.\)
\(\Rightarrow1\le m\le\dfrac{3}{2}\) ( * )
- Lại có : \(x^4-2x^2=3-2m\)
- Đặt \(f\left(x\right)=x^4-2x^2\)
- Ta có đồ thị của hàm số :
- Theo đồ thị hàm số để phương trình có nghiệm thuộc ( -2; 2 )
\(\Leftrightarrow-1\le3-2m\le8\)
\(\Leftrightarrow-\dfrac{5}{2}\le m\le2\) ( ** )
- Kết hợp điều kiện ( * ) và ( ** ) ta được : \(m\in\left[1;\dfrac{3}{2}\right]\)
Vậy có 1 giá trị m thỏa mãn điều kiện đề bài ( m = 1 ) .
Đúng 1
Bình luận (0)
Có tất cả bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-2018;2019] để hàm số
y
m
x
4
+
m
+
1
x
2
+
1
có đúng một điểm cực đại? A. 0 B. 2018 C. 1 D. 2019
Đọc tiếp
Có tất cả bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-2018;2019] để hàm số y = m x 4 + m + 1 x 2 + 1 có đúng một điểm cực đại?
A. 0
B. 2018
C. 1
D. 2019
Có tất cả bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-2019;2019] sao cho hàm số
y
x
3
-
6
x
2
+
9
-
m
x
+
2
x
-...
Đọc tiếp
Có tất cả bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-2019;2019] sao cho hàm số y = x 3 - 6 x 2 + 9 - m x + 2 x - 2 có 5 điểm cực trị?
A. 2019
B. 2021
C. 2022
D. 12
Có tất cả bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-2018;2019] để hàm số y = m x 4 + ( m + 1 ) x 2 + 1 có đúng một điểm cực đại?
A. 0
B. 2018
C. 1
D. 2019
Có tất cả bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-3; 3] để phương trình
(
m
2
+
2
)
c
o
s
2
x
-
2
m
sin
2
x
+
1
0
có nghiệm A. 3 B. 7 C. 6 D. 4
Đọc tiếp
Có tất cả bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-3; 3] để phương trình ( m 2 + 2 ) c o s 2 x - 2 m sin 2 x + 1 = 0 có nghiệm
A. 3
B. 7
C. 6
D. 4