Phương trình tiếp tuyến của hàm số y = x 3 - 2 x + 1 tại M(0;1) là:
A. y=x+1
B. y=-2x+1
C. y=3x+1
D. Đáp án khác
Những câu hỏi liên quan
Cho hàm số y= f(x)=x^3-2x^2 (C) a) Tìm f'(x). Giải bất phương trình f'(x)>0 b) Viết phương trình tiếp tuyến của (C) tại điểm M có hoành độ x0=2
Cho hàm số y = f(x)=x^3-2x^2(C) a) tìm f'(x) . Giải bất phương trình f'(x)>0 b) viết phương trình tiếp tuyến của (C) tại điểm M có hoành độ x0=2
\(f'\left(x\right)=3x^2-4x\)
\(f'\left(x\right)>0\Leftrightarrow3x^2-4x>0\Rightarrow\left[{}\begin{matrix}x>\dfrac{4}{3}\\x< 0\end{matrix}\right.\)
\(f'\left(2\right)=4\) ; \(f\left(2\right)=0\)
Phương trình tiếp tuyến:
\(y=4\left(x-2\right)+0\Leftrightarrow y=4x-8\)
Đúng 1
Bình luận (0)
Cho hàm số \(y=-x^3+3x-2\) (C)
a) Khảo sát và vẽ đồ thị hàm số
b) Tìm m để phương trình: \(x^3-3x+2m+1=0\) có 3 nghiệm phân biệt
c) Viết phương trình tiếp tuyến với (C) tại điểm có hoành độ \(x=0\)
Cho hàm số y-x^2+3x-2 có đồ thị (D)
a;Tính đạo hàm của hàm số tại điểm y,x_0 thuộc R
b,Viết phương trình tiếp tuyến của (P) tại điểm có hoành độ x_02
c,Viết phương trình tiếp tuyến của (P) tại điểm có tung độ y_00;
d, Viết phương trình tiếp tuyến của (P) biết tiếp tiếp vuông góc với đường thẳng yx+3
Đọc tiếp
Cho hàm số \(y=-x^2+3x-2\) có đồ thị (D) a;Tính đạo hàm của hàm số tại điểm y',\(x_0\) thuộc R b,Viết phương trình tiếp tuyến của (P) tại điểm có hoành độ \(x_0=2\) c,Viết phương trình tiếp tuyến của (P) tại điểm có tung độ \(y_0=0\); d, Viết phương trình tiếp tuyến của (P) biết tiếp tiếp vuông góc với đường thẳng y'=x+3
a. \(y'\left(x_0\right)=-2x_0+3\)
b. phương trình tiếp tuyến tại x0 =2 là
\(y=y'\left(x_0\right)\left(x-x_0\right)+y_0=-\left(x-2\right)+0\text{ hay }y=-x+2\)
c.\(y_0=0\Rightarrow\orbr{\begin{cases}x_0=1\\x_0=2\end{cases}\Rightarrow PTTT\orbr{\begin{cases}y=x-1\\y=-x+2\end{cases}}}\)
d. vì tiếp tuyến vuông góc với đường thẳng có hệ số góc bằng 1 nên tiếp tuyến có hệ số góc = -1
hay \(-2x_0+3=-1\Leftrightarrow x_0=2\Rightarrow PTTT:y=-x+2\)
cho đồ thị hàm số y=f(x),y=g(x) cùng tiếp xúc với đường thẳng (d):2x-y+1=0 tại M(1,3). Lập phương trình tiếp tuyến với đồ thị hàm số h(x)=f(x)*g(x)+2021x tại điểm có hoành độ bằng 1
cho hàm số \(y=x^3-3x-1\)
viết phương trình tiếp tuyến của hàm số tại điểm A(0;-1)
đây là dạng toán viết phương trình tiếp tuyến tại một điểm A(a,b)
ta là như sau:
bước 1: tính y'
bước 2: tính y'(a)
bước 3: áp dụng công thức y=y'(a)(x-a)+b
áp dụng vào bài trên ta có
\(y'=3x^2-3\)
\(y'\left(0\right)=-3\)
vậy phương trình tiếp tuyến của đồ thị có dạng
\(y=-3\left(x-0\right)+\left(-1\right)=-3x-1\)
Đúng 0
Bình luận (0)
Phương trình tiếp tuyến của đồ thị hàm số
y
x
+
x
2
+
1
tại điểm có hoành độ x 0 là: A. y x + 1 B. y x +
2
C. y x
-
1 D. y x
-
2
Đọc tiếp
Phương trình tiếp tuyến của đồ thị hàm số y = x + x 2 + 1 tại điểm có hoành độ x = 0 là:
A. y = x + 1
B. y = x + 2
C. y = x - 1
D. y = x - 2
Đáp án A.
Phương pháp: Phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm có hoành độ x = x0 là 
Cách giải: TXĐ: D = R
Ta có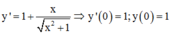 
=>Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x = 0 là: 
Đúng 0
Bình luận (0)
Viết phương trình tiếp tuyến của đồ thị hàm số
y
x
-
1
x
+
2
tại điểm
M
1
;
0
A. ...
Đọc tiếp
Viết phương trình tiếp tuyến của đồ thị hàm số y = x - 1 x + 2 tại điểm M 1 ; 0
A. y = 1 3 x - 1 3
B. y = 1 3 x + 1
C. y = x - 1
D. y = 1 9 x - 1 9
Chọn A.
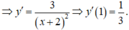
Phương trình tiếp tuyến cần tìm là: y = 1 3 x - 1 3
Đúng 0
Bình luận (0)
Viết phương trình tiếp tuyến của đồ thị hàm số y=x3 - 6x2 + 9x - 2 tại điểm có hoành độ x0 thỏa mãn phương trình y''(x0) = -12
Cho hàm số
y
x
+
2
2
x
+
3
1
. Viết phương trình tiếp tuyến của đồ thị hàm số (1), biết tiếp tuyến đó cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A, B và tam giác OAB cân tại gốc tọa độ 0. A: x + y 0 B: x + y + 2 0 C: x + y – 2 0 D: Cả A và C đúng
Đọc tiếp
Cho hàm số y = x + 2 2 x + 3 1 . Viết phương trình tiếp tuyến của đồ thị hàm số (1), biết tiếp tuyến đó cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A, B và tam giác OAB cân tại gốc tọa độ 0.
A: x + y = 0
B: x + y + 2 = 0
C: x + y – 2 = 0
D: Cả A và C đúng
