Bài 2: a)Viết phương trình đường thẳng (d1) đi qua A(2;-3) và B(1;-3)
b) Cho (d2)y=mx+2 . Xác định để (d2) song song với (d1)
Bài 1: Viết phương trình đường thẳng (d) đi qua điểm M(-2;0) và cắt trục tung tại điểm có tung độ bằng 3
Bài 2:a) Viết pt đường thẳng (d1) đi qua A(-2;3) và B(1;-3)
b) Cho (d2): y = mx+2. Xác định m để (d2) song song vs (d1)
Bài 3: Cho hàm số y=(m-2)x +(n+2) (d). Hãy xác định gía trị của m,n để đg thẳng (d) cắt trục tung tại điểm có tung độ = -2 và cắt trục hoành tại điểm có hoành độ =1
Bài 30: Cho hàm số y=x+4 (d) . Lập phương trình (d1) , biết đường thẳng (d1) đi qua điểm M(-3;-1) và song song với đường thẳng (d)
Bài 31:Viết phương trình đường thẳng (d) biết rằng đường thẳng (d) cắt trục tung tại điểm có tung độ bằng -1 và song song với đường thẳng y=5x+4
(Giúp mình 2 bài này nha)
Bài 31:
Vì (d)//y=5x+4 nên a=5
=>(d): y=5x+b
Thay x=0 và y=-1 vào (d), ta được:
b+5*0=-1
=>b=-1
viết phương trình đường thẳng (d) đi qua A(-2;3) và có cùng hệ số góc với đường thẳng 2x -y+3=0
Phương trình đườn thẳng (d) sẽ có dạng là: (d): y=ax+b(a≠0)
Ta có: 2x-y+3=0
\(\Leftrightarrow-y+2x+3=0\)
\(\Leftrightarrow-y=-2x-3\)
\(\Leftrightarrow y=2x+3\)
Vì (d) có cùng hệ số góc với đường thẳng 2x-y+3=0 nên a=2
hay (d): y=2x+b
Vì (d) đi qua A(-2;3) nên Thay x=-2 và y=3 vào hàm số y=2x+b, ta được:
\(2\cdot\left(-2\right)+b=3\)
\(\Leftrightarrow b-4=3\)
hay b=7
Vậy: (d): y=2x+7
Trong mặt phẳng Oxy, cho I(-1;2), M(-3;5).
a) Viết phương trình đường tròn (C) có tâm I và đi qua M.
b) Tìm m để đường thẳng (\(\Delta\)): 2x + 3y + m = 0 tiếp xúc với (C).
c) Viết phương trình tiếp tuyến của (C) tại 2 giao điểm A, B của (C) và (d): x - 5y - 2 = 0.
d) Tìm điểm C để tam giác ABC vuông và nội tiếp (C).
b, \(d\left(I;\Delta\right)=R\Leftrightarrow\dfrac{\left|-2+6+m\right|}{\sqrt{13}}=\sqrt{13}\)
\(\Rightarrow\left[{}\begin{matrix}m=9\\m=-17\end{matrix}\right.\)
c, Dễ tìm được tọa độ A, B: \(\left\{{}\begin{matrix}A=\left(-3,-1\right)\\B=\left(2,0\right)\end{matrix}\right.\)
Phương trình tiếp tuyến tại A có dạng: \(\Delta_1:ax+by+3a+b=0\left(a^2+b^2\ne0\right)\)
Ta có: \(d\left(I,\Delta_1\right)=\dfrac{\left|-a+2b+3a+b\right|}{\sqrt{a^2+b^2}}=\sqrt{13}\)
\(\Leftrightarrow\left(2a+3b\right)^2=13a^2+13b^2\)
\(\Leftrightarrow4a^2+9b^2+12ab=13a^2+13b^2\)
\(\Leftrightarrow9a^2+4b^2-12ab=0\)
\(\Leftrightarrow9a^2+4b^2-12ab=0\)
\(\Leftrightarrow3a=2b\)
\(\Rightarrow\Delta_1:2x+3y+9=0\)
Tương tự tiếp tuyến tại B: \(\Delta_2:3x-2y-6=0\)
a, \(R=IM=\sqrt{\left(-3+1\right)^2+\left(5-2\right)^2}=\sqrt{13}\)
Phương trình đường tròn: \(\left(x+1\right)^2+\left(y-2\right)^2=13\)
Bài 28 : Xác định hệ số a và b của hàm số y=ax+b , biết đồ thị của hàm số là đường thẳng song song với đường thẳng y=2x+2017 và đi qua điểm A(-1;3)
Bài 29 : Viết phương trình đường thẳng (d) đi qua điểm M(1;2) và song song với đường thẳng (d') : y=-2x+3
(Giúp mình 2 bài này nha)
Bài 28:
Ta có hàm số y=ax+b song song với đường thẳng y=2x+2017\(\Rightarrow\)\(\left\{{}\begin{matrix}a=2\\b\ne2017\end{matrix}\right.\)
Vậy hàm số bây giờ có dạng y=2x+b
Ta lại có hàm số y=2x+b đi qua điểm A(-1;3)\(\Rightarrow3=2.\left(-1\right)+b\Leftrightarrow b=5\)(tm)
Vậy hàm số đã cho là: y=2x+5
Bài 29:
Gọi phương trình đường thẳng cần tìm là y=ax+b(d)
Ta có hàm số y=ax+b song song với đường thẳng(d'): y=-2x+3\(\Rightarrow\)\(\left\{{}\begin{matrix}a=-2\\b\ne3\end{matrix}\right.\)
Vậy phương trình đường thẳng bây giờ có dạng y=-2x+b
Ta lại có đường thẳng y=-2x+b đi qua điểm M(1;2)\(\Rightarrow2=-2.1+b\Leftrightarrow b=4\)
Vậy phương trình đường thẳng (d) có dạng y=-2x+4
Bài 1. Lập phương trình elip qua N(3√3/2 ; 1) và độ dài tiêu cự bằng 2c=√5
Bài 2 . Lập phương trình đường tròn qua 2 điểm A( 1;1) , B(-2;-2) và tiếp xúc với đường thẳng : y+2=0
Trong mặt phẳng với hệ trục tọa đô Oxy , cho hai đường thẳng ∆1: x- y+ 1= 0 và ∆2: 2x + y-1 = 0 và điểm P (2;1) .Viết phương trình đường thẳng đi qua điểm P và cắt hai đường thẳng ∆1, ∆2 lần lượt tại hai điểm A: B sao cho P là trung điểm AB?
A. 4x – y- 7 = 0
B. x+ 4y- 4= 0
C. x- 4y-7= 0
D . 2x + y- 7= 0
Đáp án A
Ta có 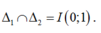
Vì A thuộc ∆1 nên A( a; a+ 1).
Vì P( 2;1) là trung điểm của đoạn AB nên B( 4-a; 1-a).
Mặt khác:
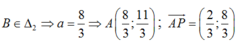
Đường thẳng AP có VTPT ( 4;-1) và qua P(2;1) nên có phương trình:
4x – y- 7 = 0
Trong mp tọa độ cho A(-2;2) và đường thẳng d1 có phương trình y = -2 x -2
A , cm A thuộc d1
b, Tìm giá trị của a để parabon (P) :y = ax2 đi qqua A
C, viết pt đường thẳng d2 đi qua A và vuông góc đường thẳng d1
D, gọi A,B là giao của (P) và d2 và C là giao của d1 với trục tung tìm tọa độ của B, C .Tính diện tích ABC
a/ Thay tọa độ A vào pt d1:
\(-2.\left(-2\right)-2=2\Leftrightarrow2=2\) (thỏa mãn)
\(\Rightarrow A\in d_1\)
b/ Để (P) qua A
\(\Rightarrow a.\left(-2\right)^2=2\Rightarrow a=\frac{1}{2}\)
c/ Gọi pt d2 có dạng \(y=kx+b\)
Do d2 vuông góc d1 \(\Rightarrow k.\left(-2\right)=-1\Rightarrow k=\frac{1}{2}\Rightarrow y=\frac{1}{2}x+b\)
Do d2 qua A nên:
\(\frac{1}{2}.\left(-2\right)+b=2\Rightarrow b=3\)
Phương trình d2: \(y=\frac{1}{2}x+3\)
d/ Tọa độ C là: \(x=0\Rightarrow y=-2.0-2=-2\Rightarrow C\left(0;-2\right)\)
Phương trình hoành độ giao điểm (P) và d2:
\(\frac{1}{2}x^2=\frac{1}{2}x+3\Rightarrow x^2-x-6=0\Rightarrow\left[{}\begin{matrix}x=-2\\x=3\end{matrix}\right.\)
\(\Rightarrow B\left(3;\frac{9}{2}\right)\)
\(\Rightarrow AB=\sqrt{\left(3+2\right)^2+\left(\frac{9}{2}-2\right)^2}=\frac{5\sqrt{5}}{2}\)
\(AC=\sqrt{\left(0+2\right)^2+\left(-2-2\right)^2}=2\sqrt{5}\)
\(S_{ABC}=\frac{1}{2}AB.AC=\frac{25}{2}\)
Bài 26 : Biết đường thẳng (d):y=ax+b đi qua điểm M(2;\(\dfrac{1}{2}\)) và song song với đường thẳng (d') 2x+y=3 . Tìm các hệ số a và b
Bài 27 : Xác định phương trình của đường thẳng (d) cắt trục tung tại điểm có tung độ bằng 6 và cắt trục hoành tại điểm có hoành độ bằng -3
Giúp mình 2 bài này nha
Bài 27:
Vì (d) đi qua A(-3;0) và B(0;6) nên ta có hệ:
0a+b=6 và -3a+b=0
=>b=6 và b=3a
=>a=2 và b=6