Cho hình vuông ABCD có M;N là trung điểm của BC;CD.tìm đỉnh B biết điểm N (0;-2) và AM có pt :x+2y-2=0 và cạnh hình vuông bằng 4
m.n giúp mk với ; các cậu thử giải tìm xem có bao nhiêu điểm M nhé thank nhiều
Những câu hỏi liên quan
Cho hình vuông ABCD biết diện tích hình vuông có cạnh gấp đôi hình vuông ABCD là 144 m2. Hỏi hình vuông có cạnh gấp 3 lần hình ABCD có diện tích bao nhiêu m2 ?
Cạnh hình vuông gấp đôi hay gấp 3 v
Cho hình vuông ABCD. Biết diện tích của hình vuông có cạnh gấp đôi cạnh hình vuông ABCD là 144m2. Hỏi hình vuông có cạnh gấp 3 lần cạnh hình vuông ABCD cò diện tích bao nhiu m2
Cho hình vuông ABCD có cạnh 20 m. Hãy xác định điểm E trên cạnh AB sao cho diện tích hình thang vuông BCDE bằng
3
4
diện tích vuông ABCD A. Điểm E ở trên cạnh AB sao cho BE 8 m B. Điểm E ở trên cạnh AB sao cho BE 6 m C. Điểm E ở trên cạnh AB sao cho BE 12 m D. Điểm E là trung điểm của AB
Đọc tiếp
Cho hình vuông ABCD có cạnh 20 m. Hãy xác định điểm E trên cạnh AB sao cho diện tích hình thang vuông BCDE bằng 3 4 diện tích vuông ABCD
A. Điểm E ở trên cạnh AB sao cho BE = 8 m
B. Điểm E ở trên cạnh AB sao cho BE = 6 m
C. Điểm E ở trên cạnh AB sao cho BE = 12 m
D. Điểm E là trung điểm của AB
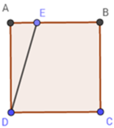
Gọi BE = x (m).
Diện tích hình vuông ABCD là: SABCD = AB2 = 202 = 400 (m2)
Diện tích hình thang vuông BCDE là:
SBCDE = ( B E + D C ) B C 2 = ( x + 20 ) .20 2 = 10(x + 20)
Vì diện tích hình thang vuông BCDE bằng 3 4 diện tích hình vuông ABCD nên ta có:
SBCDE = 3 4 SABCD = 10(x + 20) = 3 4 .400 óx + 20 = 30 ó x = 10 (m)
Vậy điểm E ở trên cạnh AB sao cho BE = 10 m hay E là trung điểm đoạn AB.
Đáp án cần chọn là: D
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy, cho hình vuông ABCD có đình M(-–-3;5), tâm I thuộc đường thẳng d : y =−x+5 và diện tích của hình vuông ABCD bằng 25 . Tim tọa độ các đỉnh của hình vuông ABCD, biết rằng tâm I có hoành độ dương
Cho hình vuông ABCD. Biết diện tích của hình vuông có cạnh gấp đôi cạnh hình vuông ABCD là 144 m2. Hỏi hình vuông có cạnh gấp 3 lần cạnh hình ABCD có diện tích là bao nhiêu. (Giải chi tiết hộ em nhé. Đừng liên quan tới số thập phân nhé.)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a; SASBSCSDa√2; O là tâm của hình vuông ABCD.a) C/m (SAC) và (SBD) cùng vuông góc với (ABCD). b) C/m (SAC) ⊥(SBD)c) Tính khoảg cách từ S đến (ABCD)d) Tính góc giữa đường SB và (ABCD).e) Gọi M là trung điểm của CD, hạ OH⊥SM, chứng minh H là trực tâm tam giác SCDf) Tính góc giưa hai mặt phẳng (SCD) và (ABCD)g) Tính khoảng cách giữa SM và BC; SM và AB.
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a; SA=SB=SC=SD=a√2; O là tâm của hình vuông ABCD.
a) C/m (SAC) và (SBD) cùng vuông góc với (ABCD).
b) C/m (SAC) ⊥(SBD)
c) Tính khoảg cách từ S đến (ABCD)
d) Tính góc giữa đường SB và (ABCD).
e) Gọi M là trung điểm của CD, hạ OH⊥SM, chứng minh H là trực tâm tam giác SCD
f) Tính góc giưa hai mặt phẳng (SCD) và (ABCD)
g) Tính khoảng cách giữa SM và BC; SM và AB.
a: SO vuông góc (ABCD)
=>(SAC) vuông góc (ABCD)
SO vuông góc (ABCD)
=>(SBD) vuông góc (ABCD)
b: BD vuông góc AC
BD vuông góc SA
=>BD vuông góc (SAC)
d: (SB;(ABCD))=(BS;BO)=góc SBO
cos SBO=OB/SB=a*căn 2/2/(a*căn 2)=1/2
=>góc SBO=60 độ
Đúng 0
Bình luận (0)
cho hình vuông abcd . biết diện tích của hình vuông có cạnh gấp đôi cạnh hình vuông abcd là 144 m2 . hỏi có bao nhiêu m2?
cho hình vuông abcd có cạnh 4cm.trên các cạnh có hình vuông lấy lần lượt các điểm chính giữa m n p q .nối bốn diểm đó được hình tứ giác mnpq.tính tỉ số của diện tích hình tứ giác và hình vuông abcd
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, SA vuông góc (ABCD). AH, AK lần lượt là đường cao của tam giác SAB, SAD.
a/ C/m: CD vuông góc SD và AK vuông góc SC.
b/ C/m: SC vuông góc (AHK).
c) Tính góc giữa SO với (ABCD)
d) Tính góc giữa SO với (SAB)
e) Tính khoảng cách từ B đến (SCD)
f) Tính khoảng cách từ H đến (SAC)
a: CD vuông góc DA
CD vuông góc SA
=>CD vuông góc (SAD)
=>CD vuông góc SD
b: CD vuông góc AK
AK vuông góc SD
=>AK vuông góc (SCD)
=>SC vuông góc AK
BC vuông góc AH
AH vuông góc SB
=>AH vuông góc SC
=>SC vuông góc (AKH)
c: (SO;(ABCD))=(OS;OA)=góc SOA
Đúng 0
Bình luận (0)
1.Cho hình thoi ABCD có cạnh =a.Biết góc B=60 độ
a)C/m tam giác ABC đều
b)Tính diện tích hình thoi ABCD theo a
2.Cho hình vuông ABCD có độ dài cạnh =a.Điểm M bất kì trên đường thẳng AC.Kẻ ME vuông góc AB tại E và MF vuông góc AC tại F.Tìm vị trí của điểm M trên AC để diện tích tam giác CEF lớn nhất
1) hình tự vẽ nhé
a) Vì ABCD là hình thoi (gt)
\(\Rightarrow AB=BC\left(đn\right)\)
\(\Rightarrow\Delta ABC\)cân tại B
Mà \(\widehat{B}=60^0\)
\(\Rightarrow\Delta ABC\)là tam giác đều
b) Vì \(\Delta ABC\)đều(cmt)\(\Rightarrow AB=BC=AC=a\)
Gọi O là giao điểm 2 đường chéo BD và AC
Vì ABCD là hình thoi (gt) \(\Rightarrow DB\perp AC\left(tc\right)\)
\(\Rightarrow BO\perp AC\)
Vì tam giác ABC đều mà trong tam giác ABC thì BO là đường cao ứng với cạnh AC
\(\Rightarrow BO\)là đường trung tuyến ứng vs cạnh AC(tc)
\(\Rightarrow O\)là trung điểm của AC
\(\Rightarrow AO=OC=\frac{1}{2}AC=\frac{1}{2}a\)
Áp dụng định lý Py-ta-go vào tam giác BOC vuông tại O ta được:
\(BO^2+OC^2=BC^2\)
\(BO^2+\frac{1}{4}a^2=a^2\)
\(BO^2=\frac{3}{4}a^2\)
\(\Rightarrow BO=\frac{\sqrt{3}}{2}a\)
Ta có: \(S_{ABC}=\frac{1}{2}BO.AC=\frac{1}{2}.\frac{\sqrt{3}a}{2}.a\)
\(=\frac{\sqrt{3}}{4}a^2\)
CMTT \(S_{ADC}=\frac{\sqrt{3}}{4}a^2\)
\(S_{ABCD}=S_{ADC}+S_{ABC}=\frac{\sqrt{3}}{2}a^2\)