Cho hàm số y=x² ; y=2x+3 a, vẽ các đồ thị trên cùng 1 mặt phẳng tọa độ b, tìm hoành độ giao điểm chung của 2 đồ thị

Những câu hỏi liên quan
Cho hàm số y= 2+ x, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y = 2 - x, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y = x - 2, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y = x + 2, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y= 2+ x, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y = 2 - x, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y = x - 2, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y = x + 2, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Bài 1. Cho hàm số y 2x-1a) Tính giá trị của hàm số y khi x0; x1; x -2b) Tìm giá trị của x khi y3Bài 2. Cho hàm số y -3xa) Vẽ đồ thị hàm sốb) Tìm trên đồ thị hàm số điểm có hoành độ bằng 2c) Tìm trên đồ thị hàm số điểm có tung độ bằng -6
Đọc tiếp
Bài 1. Cho hàm số
y= 2x-1
a) Tính giá trị của hàm số y khi x=0; x=1; x= -2
b) Tìm giá trị của x khi y=3
Bài 2. Cho hàm số
y= -3x
a) Vẽ đồ thị hàm số
b) Tìm trên đồ thị hàm số điểm có hoành độ bằng 2
c) Tìm trên đồ thị hàm số điểm có tung độ bằng -6
Bài 1:
a: x=0 => y=-1
x=1 =>y=1
Đúng 1
Bình luận (0)
Cho hàm số y f(x) Biết hàm số đã cho thỏa mãn hệ thức
∫
f
x
sin
x
d
x
-
f
x
cos
x
+
∫
π
2
cosxdx
. Hỏi hàm số y f(x) là hàm số nào trong các hàm số sau? A. . B. . C. . D. .
Đọc tiếp
Cho hàm số y = f(x)
Biết hàm số đã cho thỏa mãn hệ thức ∫ f x sin x d x = - f x cos x + ∫ π 2 cosxdx . Hỏi hàm số y = f(x) là hàm số nào trong các hàm số sau?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho các hàm số:
y
cos
x
,
y
sin
x
,
y
tan
x
,
y
c
o
t
x
.Trong các hàm số trên, có bao nhiêu hàm số chẵn? A. 1 B. 3 C. 2 D. 4
Đọc tiếp
Cho các hàm số: y = cos x , y = sin x , y = tan x , y = c o t x .
Trong các hàm số trên, có bao nhiêu hàm số chẵn?
A. 1
B. 3
C. 2
D. 4
Cho hàm số y f(x) có đồ thị của hàm số y f (x) được cho như hình bên và các mệnh đề sau: (1). Hàm số y f(x) đồng biến trên khoảng (-1;0) (2). Hàm số y f(x) nghịch biến trên khoảng (1;2) (3). Hàm số y f(x) đồng biến trên khoảng (3;5) (4). Hàm số y f(x) có hai điểm cực đại và một điểm cực tiểu.Số mệnh đề đúng là A. 1 B. 3 C. 4 D. 2
Đọc tiếp
Cho hàm số y = f(x) có đồ thị của hàm số y = f '(x) được cho như hình bên và các mệnh đề sau: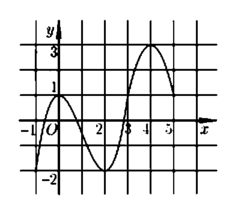
(1). Hàm số y = f(x) đồng biến trên khoảng (-1;0)
(2). Hàm số y = f(x) nghịch biến trên khoảng (1;2)
(3). Hàm số y = f(x) đồng biến trên khoảng (3;5)
(4). Hàm số y = f(x) có hai điểm cực đại và một điểm cực tiểu.
Số mệnh đề đúng là
A. 1
B. 3
C. 4
D. 2
Đáp án D
Dựa vào hình vẽ, ta thấy rằng
+ Đồ thị hàm số f '(x) cắt Ox tại 3 điểm phân biệt x 1 - 1 ; 0 , x 2 0 ; 1 , x 3 2 ; 3
Và f '(x) đổi dấu từ - → + khi đi qua x 1 , x 3 ⇒ Hàm số có 2 điểm cực tiểu, 1 điểm cực đại
+ Hàm số y = f(x) nghịch biến trên khoảng - 1 ; x 1 đồng biến trên x 1 ; x 2 (1) sai
+ Hàm số y = f(x) nghịch biến trên khoảng x 2 ; x 3 (chứa khoảng (1;2)), đồng biến trên khoảng x 3 ; 5 (chứa khoảng (3;5)) ⇒ 2 ; 3 đúng
Vậy mệnh đề 2,3 đúng và 1, 4 sai.
Đúng 0
Bình luận (0)
Cho hàm số y f( x) có đạo hàm liên tục trên R, hàm số y f’ (x-2) có đồ thị hàm số như hình bên. Số điểm cực trị của hàm số y f( x) là : A. 0 B. 2 C. 1 D. 3
Đọc tiếp
Cho hàm số y= f( x) có đạo hàm liên tục trên R, hàm số y= f’ (x-2) có đồ thị hàm số như hình bên. Số điểm cực trị của hàm số y= f( x) là :
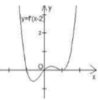
A. 0
B. 2
C. 1
D. 3
Ta có: f' (x - 2) = f' (x).(x-2)' = f'(x)
Do đó; đồ thị hàm số y= f’ (x) có hình dạng tương tự như trên.
Đồ thị hàm số y= f( x-2) có 3 điểm cực trị khi và chỉ khi đồ thị hàm số y= f( x) cũng có 3 điểm cực trị.
Chọn D.
Đúng 0
Bình luận (0)
Cho hàm số y f(x) có đạo hàm liên tục trên R, hàm số y f’(x – 2) có đồ thị hàm số như hình bên. Số điểm cực trị của hàm số y f(x) là : A. 0 B. 2 C. 1 D. 3
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm liên tục trên R, hàm số y = f’(x – 2) có đồ thị hàm số như hình bên. Số điểm cực trị của hàm số y = f(x) là :
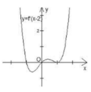
A. 0
B. 2
C. 1
D. 3
Đáp án D
Phương pháp : Nhận xét : f’(x – 2) = f’(x)
Cách giải : Ta có : f’(x – 2) = (x – 2)’. f’(x) = f’(x) → Đồ thị hàm số y = f’(x) có hình dạng tương tự như trên.
Đồ thị hàm số y = f(x – 2)có 3 điểm cực trị => Đồ thị hàm số y = f(x) cũng có 3 điểm cực trị
Đúng 0
Bình luận (0)
a/ cho hàm số: y=(-3m - 2)x2. Tìm m để hàm số nghịch biến khi x < 0
b/ cho hàm số: y=(m2 - 2m + 3)x2. Xác định tính biến thiên của hàm số
c/ cho hàm số: y=(2m + 3)x2. Tìm m để hàm số đồng biến khi x>0
a.
Hàm số nghịch biến khi \(x< 0\Rightarrow-3m-2>0\Rightarrow m< -\dfrac{2}{3}\)
b.
Do \(a=m^2-2m+3=\left(m-1\right)^2+2>0;\forall m\)
\(\Rightarrow\) Hàm đồng biến khi \(x>0\) và nghịch biến khi \(x< 0\)
c.
Hàm đồng biến khi \(x>0\Rightarrow2m+3>0\)
\(\Rightarrow m>-\dfrac{3}{2}\)
Đúng 1
Bình luận (0)
Cho hai hàm số y f(x) và y g(x) xác định trên R. Đặt S(x) f(x) + g(x) và P(x) f(x) g(x).Xét các mệnh đề:i) Nếu y f(x) và y g(x) là những hàm số chẵn thì y S(x) và y P(x) cũng là những hàm số chẵnii) Nếu y f(x) và y g(x) là những hàm số lẻ thì y S(x) là hàm số lẻ và y P(x) là hàm số chẵniii) Nếu y f(x) là hàm số chẵn, y g(x) là hàm số lẻ thì y P(x) là hàm số lẻSố mệnh đề đúng là: A. 1 B. 2 C. 3 D. Tất cả đều sai
Đọc tiếp
Cho hai hàm số y = f(x) và y = g(x) xác định trên R. Đặt S(x) = f(x) + g(x) và P(x) = f(x) g(x).
Xét các mệnh đề:
i) Nếu y = f(x) và y = g(x) là những hàm số chẵn thì y = S(x) và y = P(x) cũng là những hàm số chẵn
ii) Nếu y = f(x) và y = g(x) là những hàm số lẻ thì y = S(x) là hàm số lẻ và y = P(x) là hàm số chẵn
iii) Nếu y = f(x) là hàm số chẵn, y = g(x) là hàm số lẻ thì y = P(x) là hàm số lẻ
Số mệnh đề đúng là:
A. 1
B. 2
C. 3
D. Tất cả đều sai