Cho d : x=1+t ; y=2+t . Tìm I trên d sao cho tam giác AIO vuông góc tại I . Biết điểm A(0,-3)

Những câu hỏi liên quan
Cho biểu thức D = (2x^2+1/x^3-1 - 1/x-1) : ( 1 - x^2+3/x^2+x+1)
a) Rút gọn D
b) Tìm giá trị của x để D = 3
c) Tìm những giá trị của x để D < 0
d) Tìm GTNN của biểu thức D biết x > 2
Xem chi tiết
1.cho biểu thức
|D=(1/x-1-x/1-x^3-x^2+x+1/x+1):2x+1/x^2+x+1)
a)rút gọn D
b)tính gtri của D
c)tìm gtri nguyên của x để biểu thức D có gtri nguyên
2) Cho biểu thức D = (1+\(\frac{x}{x^2+1}\)) : (\(\frac{1}{x-1}-\frac{2x}{x^3+x-x^2-1}\))
a. Rút gọn biểu thức D
b. Tìm giá trị của x sao cho D < 1
c. Tìm giá trị nguyên của x để D có giá trị nguyên
ĐK : x \(\ne\) 1
a) D = \(\left(1+\frac{x}{x^2+1}\right):\left(\frac{1}{x-1}-\frac{2x}{x^3+x-x^2-1}\right)=\left(\frac{x^2+1}{x^2+1}+\frac{x}{x^2+1}\right):\left(\frac{x^2+1}{\left(X^2+1\right)\left(x-1\right)}-\frac{2x}{x^2\left(x-1\right)+\left(x-1\right)}\right)\)
\(=\frac{x^2+x+1}{x^2+1}:\frac{x^2-2x+1}{\left(x-1\right)\left(x^2+1\right)}=\frac{x^2+x+1}{x^2+1}\cdot\frac{\left(x-1\right)\left(X^2+1\right)}{\left(x-1\right)^2}=\frac{x^2+x+1}{x^2+1}\cdot\frac{x^2+1}{x-1}=\frac{x^2+x+1}{x-1}\)
b)
D <1
=> \(x^2+x+1< x-1\Rightarrow x^2+x+1-x+1< 0\Rightarrow x^2+2< 0\) ( vô lí )
Vậy D > 1, không có x thỏa mãn
c) D thuộc Z
=> \(\frac{x^2+x+1}{x-1}=\frac{x^2-x+2x-2+3}{x-1}=\frac{x\left(x-1\right)+2\left(x-1\right)+3}{x-1}=x+2+\frac{3}{x-1}\)
Vì x thuộc Z nên D thuộc Z khi
\(x-1\inƯ\left(3\right)=\left\{\pm1;\pm3\right\}\)
* x -1 = 1 => x= 2 (tm)
* x-1 = -1 => x = 0 (tm)
* x-1 =3 => x = 4 (tm)
* x-1 = -3 => x = -2 ( tm )
Đúng 0
Bình luận (0)
\(ĐKXD:x\ne1\)
\(a,D=\left(1+\frac{x}{x^2+1}\right):\left(\frac{1}{x-1}-\frac{2x}{x^3+x-x^2-1}\right)=\frac{x^2+x+1}{x^2+1}:\left(\frac{1}{\left(x-1\right)}-\frac{2x}{\left(x-1\right)\left(x^2+1\right)}\right)=\frac{x^2+x+1}{x^2+1}:\left(\frac{x^2+1}{\left(x-1\right)\left(x^2+1\right)}-\frac{2x}{\left(x-1\right)\left(x^2+1\right)}\right)=\frac{x^2+x+1}{x^2+1}:\left(\frac{x^2-2x+1}{\left(x-1\right)\left(x^2+1\right)}\right)=\frac{x^2+x+1}{x^2+1}:\frac{\left(x-1\right)^2}{\left(x-1\right)\left(x^2+1\right)}=\frac{x^2+x+1}{x^2+1}:\frac{x-1}{x^2+1}=\frac{\left(x^2+x+1\right)\left(x^2+1\right)}{\left(x^2+1\right)\left(x-1\right)}=\frac{x^2+x+1}{x-1}\)
\(D< 1\Leftrightarrow x^2+x+1< x-1\Leftrightarrow\left(x-1\right)-\left(x^2+x+1\right)>0\Leftrightarrow x-1-x^2-x-1>0\Leftrightarrow-\left(x^2+2\right)>0\left(\text{ vô lí}\right).\text{ Nên không tìm được x thỏa mãn}\)
\(ĐểDnguyênthì:x^2+x+1⋮x-1\Leftrightarrow x\left(x-1\right)+2x+1⋮x-1\Leftrightarrow\left(x+2\right)\left(x-1\right)+3⋮x-1\Leftrightarrow3⋮x-1\left(\text{ vì: (x+2)(x-1) chia hết cho x-1}\right)\Leftrightarrow x-1\in\left\{-1;1;-3;3\right\}\Leftrightarrow x\in\left\{0;2;-2;4\right\}.Vậy:x\in\left\{0;2;-2;4\right\}thìDnguyên\)
Đúng 0
Bình luận (0)
Cho biểu thức D=((x2+2)/(x3+1)-1/(x+1))*(4x/3)
a) Rút gọn biểu thức
b) Tính GTBT tại x=1/2
c) Tìm x để D=8/9
d) Tìm giá trị lớn nhất của D khi x>0
a: \(D=\left(\dfrac{x^2+2}{x^3+1}-\dfrac{1}{x+1}\right)\cdot\dfrac{4x}{3}\)
\(=\dfrac{x^2+2-x^2+x-1}{\left(x+1\right)\left(x^2-x+1\right)}\cdot\dfrac{4x}{3}\)
\(=\dfrac{x+1}{\left(x+1\right)\left(x^2-x+1\right)}\cdot\dfrac{4x}{3}\)
\(=\dfrac{4x}{3\left(x^2-x+1\right)}\)
b: Thay x=1/2 vào D, ta được:
\(D=\left(4\cdot\dfrac{1}{2}\right):\left[3\cdot\left(\dfrac{1}{4}-\dfrac{1}{2}+1\right)\right]\)
\(=2:\left[3\cdot\dfrac{1-2+4}{4}\right]\)
\(=2:\left[3\cdot\dfrac{3}{4}\right]=2:\dfrac{9}{4}=\dfrac{8}{9}\)
c: Ta có: D=8/9
nên \(\dfrac{4x}{3\left(x^2-x+1\right)}=\dfrac{8}{9}\)
\(\Leftrightarrow24\left(x^2-x+1\right)=36x\)
\(\Leftrightarrow2x^2-2x+2-3x=0\)
\(\Leftrightarrow2x^2-5x+2=0\)
=>(x-2)(2x+1)=0
=>x=2 hoặc x=-1/2
Đúng 1
Bình luận (0)
Cho biểu thức:
D=\(\frac{3\left(x+1\right)}{x^3+x^2+x+1}\)
a, tìm ĐKXĐ, rút gọn D
b, Tìm x để D nguyên
c, Tìm GTLN của D
a,ĐKXĐ của biểu thức D là :
x3+x2+x+1\(\ne0\)
\(\Leftrightarrow\)x2(x+1)+(x+1)\(\ne\)0
\(\Leftrightarrow\left(x+1\right)\left(x^2+1\right)\ne0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+1\ne0\\x^2+1\ne0\left(vôlí\right)\end{matrix}\right.\)
\(\Leftrightarrow x\ne-1\)
Ta có : D=\(\frac{3\left(x+1\right)}{x^3+x^2+x+1}=\frac{3\left(x+1\right)}{x^2\left(x+1\right)+\left(x+1\right)}=\frac{3.\left(x+1\right)}{\left(x+1\right)\left(x^2+1\right)}=\frac{3}{x^2+1}\)
b,Để D nguyên thì \(\frac{3}{x^2+1}\)(đkxđ: x\(\ne-1\)) nguyên
\(\Leftrightarrow\)x2+1\(\inƯ\left(3\right)=\left\{1;-1;3;-3\right\}\)
ta có bảng giá trị sau :
| x2+1 | -1 | 1 | 3 | -3 |
| x2 | -2 | 0 | 2 | -4 |
| x | ko có giá trị | 0 | \(\sqrt{2}\) | ko có giá trị |
| So sánh điều kiện | ko tm | tm | tm | ko tm |
vậy x\(\in\left\{0;\sqrt{2}\right\}\)thì D nguyên
c, Ta có : D=\(\frac{3}{x^2+1}\left(đkxđ:x\ne-1\right)\)\(\le3\)
Dấu = xảy ra khi : x=0 \(\Leftrightarrow\)D=3
Vậy Max D=3 \(\Leftrightarrow x=0\)
Đúng 0
Bình luận (0)
Cho hai đường thẳng
d
:
x
1
-
t
y
t
z
-
t
và
d
:...
Đọc tiếp
Cho hai đường thẳng d : x = 1 - t y = t z = - t và d ' : x = 2 t ' y = - 1 + t ' z = t ' . Khẳng định nào sau đây là đúng?
![]()
![]()
![]()
![]()
Cho d: -x - 2y + 1 0;
d
x
1
-
2
t
y
3
-
t
. Vị trí tương đối của d và d’ là: A. Song song B. Trùng nhau C. vuông góc D. cắt như...
Đọc tiếp
Cho d: -x - 2y + 1 = 0; d ' = x = 1 - 2 t y = 3 - t . Vị trí tương đối của d và d’ là:
A. Song song
B. Trùng nhau
C. vuông góc
D. cắt nhưng không vuông
Đáp án: D
Ta có:
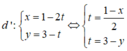
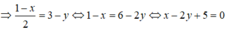
⇒ d': x - 2y + 5 = 0
Ta thấy:
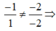 ⇒ d cắt d’
⇒ d cắt d’
Mà (-1;-2).(1;-2) = -1 + 4 = 3 ≠ 0 nên d cắt d’ nhưng không vuông
Đúng 0
Bình luận (0)
Cho A=(x-1)(x+5)-x+1
B=4x+x^2
a) Tìm x để A=0.
b) Tính B/A.
c) Tính C/D biết: B/A+C/D=(5-x)/(1-x^2).
d) Tìm x nguyên để C/D có giá trị nguyên.
Cho D=\(\left(\dfrac{2x}{x\sqrt{x}-1}-\dfrac{\sqrt{x}}{x+\sqrt{x}+1}\right)\left(\dfrac{1+x\sqrt{x}}{1+\sqrt{x}}-\sqrt{x}\right)\)
a. Rút gọn D
b. Tìm x khi D=3
a) D (ĐKXĐ: x\(\ge0,x\ne1\))
=\(\left(\dfrac{2x-\sqrt{x}\left(x+\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\right)\left(1-\sqrt{x}+x-\sqrt{x}\right)\)
=\(\dfrac{2x-x\sqrt{x}-x-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}.\left(\sqrt{x}-1\right)^2\)
\(=\dfrac{\left(x-x\sqrt{x}-\sqrt{x}\right)\left(\sqrt{x}-1\right)}{\left(x+\sqrt{x}+1\right)}\)
=\(\dfrac{\sqrt{x}\left(\sqrt{x}-x-1\right)\left(\sqrt{x}-1\right)}{\left(x+\sqrt{x}+1\right)}\)
=\(-\sqrt{x}\left(\sqrt{x}-1\right)=\sqrt{x}-x\)
b) \(\sqrt{x}-x=3\Leftrightarrow\sqrt{x}\left(1-\sqrt{x}\right)=3\)
=\(\sqrt{x}-x-3=0\Leftrightarrow\left(x-2.\dfrac{1}{2}x+\dfrac{1}{4}\right)-\dfrac{13}{4}=0\)
\(\left(\sqrt{x}-\dfrac{1}{2}\right)^2-\dfrac{13}{4}=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}-\dfrac{1}{2}=\dfrac{13}{4}\\\sqrt{x}-\dfrac{1}{2}=-\dfrac{13}{4}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{225}{16}\\x=\dfrac{121}{16}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Cho biểu thức D=\(\left(\dfrac{\sqrt{x}}{3+\sqrt{x}}+\dfrac{x+9}{9-x}\right):\left(\dfrac{3\sqrt{x}+1}{x-3\sqrt{x}}-\dfrac{1}{\sqrt{x}}\right)\)
a) tìm điều kiện
b) rút gọn
c) tìm x sao cho D < -1
a: ĐKXĐ: x>0; x<>9
b: \(D=\left(\dfrac{\sqrt{x}}{\sqrt{x}+3}-\dfrac{x+9}{x-9}\right):\dfrac{3\sqrt{x}+1-\sqrt{x}+3}{\sqrt{x}\left(\sqrt{x}-3\right)}\)
\(=\dfrac{x-3\sqrt{x}-x-9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)}{2\sqrt{x}+4}\)
\(=\dfrac{-3\left(\sqrt{x}+3\right)}{\sqrt{x}+3}\cdot\dfrac{\sqrt{x}}{2\sqrt{x}+4}=\dfrac{-3\sqrt{x}}{2\sqrt{x}+4}\)
c: Để D<-1 thì D+1<0
\(\Leftrightarrow-3\sqrt{x}+2\sqrt{x}+4< 0\)
\(\Leftrightarrow4-\sqrt{x}< 0\)
hay x>16
Đúng 0
Bình luận (0)
























