a) Thay a=3 vào hệ pt, ta được:

\(\left\{{}\begin{matrix}4x-3y=6\\-5x+3y=8\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}-x=14\\4x-3y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-14\\-56-3y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-14\\-3y=62\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=-14\\y=-\dfrac{62}{3}\end{matrix}\right.\)

Vậy: Khi a=3 thì hệ pt có nghiệm duy nhất là: \(\left(x,y\right)=\left(-14;-\dfrac{62}{3}\right)\)

a. với a=3 ta có hpt: {4x-3y=6                                                                                                          {-5x+3y=8 

    <=> {-x=14           <=> {x=-14                                                                                  {-5x+3y=8            {x= -62/3    

6x+ay=6, 2ax+by=3

Thay a=b=1 vào hệ phương trình ta có 6x+y=6, 2x+y=3

6x+y-(2x+y)=6-3

4x=3

x=3/4

y=6-6.3/4=3/2

Vì hệ có nghiệm x=1,y=5 nên ta có 6.1+a.5=6 và 2a+5b=3

a.5=0

a=0

Thay a=0 vào 2a+5b=3 ta có 0+5b=3 =>b=3/5

thay x,y vô hệ đã cho rồi giải hệ với nghiệm a,b là ra ak bạn

8-a=b

2+b=a

(a;b)=(5;3)

a. Theo bài ra ta có: \(x^2+x-2=0\)

\(\left[{}\begin{matrix}x=-2\\x=1\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}y=-\left(-2\right)+2=4\\y=-1+2=1\end{matrix}\right.\)

Vậy tọa độ giao điểm cần tìm là: \(\left(-2;4\right)\); \(\left(1:1\right)\)

b. Thay x = 2 ; y = -1 vào hpt ta có: 

\(\left\{{}\begin{matrix}8-a=b\\2+b=a\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}-a-b=-8\\-a+b=-2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}a=5\\b=3\end{matrix}\right.\)

Thay x = 1; y = −2 vào hệ ta được  2 + b ( − 2 ) = − 4 b − a ( − 2 ) = − 5

Ta coi đây là một hệ phương trình bậc nhất hai ẩn là a và b và giải hệ phương trình này

2 + b ( − 2 ) = − 4 b − a ( − 2 ) = − 5 ⇔ − 2 b = − 6 b + 2 a = − 5 ⇔ b = 3 3 + 2. a = − 5 ⇔ b = 3 a = − 4

Suy ra a + b = −4 + 3 = −1

Đáp án: A

D = a + b a − b a 3 + b 3 a 3 − b 3 = a + b a 3 − b 3 − a − b a 3 + b 3

= a + b a − b a 2 + a b + b 2 − a − b a + b a 2 − a b + b 2

= a + b a − b a 2 + a b + b 2 − a 2 + a b − b 2 = 2 a b a + b a − b

D x = 2 a − b 2 ( a 2 + b 2 ) a 3 − b 3 = 2 a 3 − b 3 − 2 a − b a 2 + b 2

= 2 a − b a 2 + a b + b 2 − 2 a − b a 2 + b 2 = 2 a b ( a − b )

D y = a + b 2 a 3 + b 3 2 ( a 2 + b 2 ) = 2 a + b a 2 + b 2 − 2 ( a 3 + b 3 )

= 2 a + b a 2 + b 2 − 2 a + b a 2 − a b + b 2 = 2 a b ( a + b )

Với a ≠ b ;   a , b ≠ 0 ⇒ D ≠ 0 , hệ phương trình có nghiệm duy nhất

x = D x D = 2 a b a − b 2 a b a − b a + b = 1 a + b x = D y D = 2 a b a + b 2 a b a − b a + b = 1 a − b

Đáp án cần chọn là: B

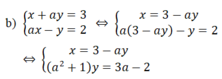
Do a 2  + 1 ≠ 0 ∀ x nên hệ phương trình trở thành:

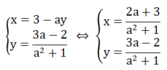
Khi đó:

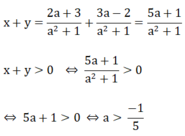
Vậy với a > (-1)/5 thì hệ phương trình có nghiệm duy nhất (x; y) thỏa mãn x+y >0

Thay x = 3; y = −4 vào hệ phương trình ta được

2 a .3 + b − 4 = − 1 b .3 − a . − 4 = 5 ⇔ 6 a − 4 b = − 1 4 a + 3 b = 5 ⇔ 12 a − 8 b = − 2 12 a + 9 b = 15 ⇔ 17 b = 17 4 a + 3 b = 5 ⇔ b = 1 a = 1 2

Vậy a = 1 2 ; b = 1

Đáp án: A