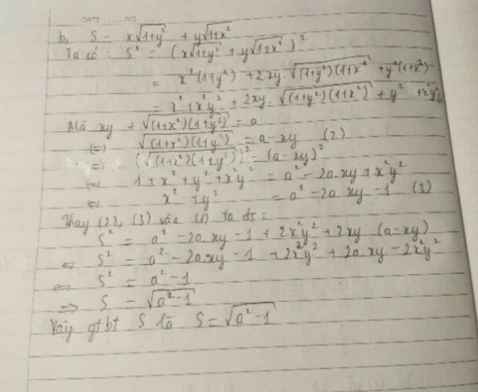Tìm giá trị của biểu thức: \(\left|x-y\right|\) biết x+y=2; xy=-1

Những câu hỏi liên quan
tìm giá trị lớn nhất của biểu thức
\(M=\dfrac{\left|x-y\right|+\left|x+y\right|+\left|xy-1\right|+\left|xy+1\right|}{\sqrt{\left(x^2+1\right)\left(y^2+1\right)}}\)
cho 2 số thực x,y thỏa mãn điều kiên \(x+y+25=8\left(\sqrt{x-1}+\sqrt{y-5}\right)\). Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức: \(P=\sqrt{\left(x-1\right)\left(y-5\right)}\)
Tìm giá trị nhỏ nhất của các biểu thức sauAx^2-4x+1 B4x^2+4x+11 Cleft(x-1right)left(x+3right)left(x+2right)left(x+6right)D2x^2+y^2-2xy+2x-4y+9 Tìm giá trị lớn nhất của các biểu thức sauE5-8x-x^2F4x-x^2+1
Đọc tiếp
Tìm giá trị nhỏ nhất của các biểu thức sau
A=\(x^2-4x+1\) \(B=4x^2+4x+11\)
\(C=\left(x-1\right)\left(x+3\right)\left(x+2\right)\left(x+6\right)\)
\(D=2x^2+y^2-2xy+2x-4y+9\)
Tìm giá trị lớn nhất của các biểu thức sau
\(E=5-8x-x^2\)
\(F=4x-x^2+1\)
BT16: Cho đơn thức \(F=\left(-\dfrac{3}{5}xy^2\right)^2.\left(\dfrac{20}{27}x^3y\right)\)
a, Thu gọn đơn thức và tìm bậc của đơn thức F
b, Tính giá trị của biểu thức F biết \(y=-\dfrac{x}{3}\)và x+y=2
a: F=9/25x^2y^4*20/27x^3y=4/15x^5y^5
Bậc: 10
b: y=-x/3 và x+y=2
=>x+y=2 và -1/3x-y=0
=>x=3 và y=-1
Khi x=3 và y=-1 thì F=4/15*(-3)^5=-324/5
Đúng 2
Bình luận (0)
Gỉa sử x,y là các số dương thỏa mãn đẳng thức x+y=\(\sqrt{10}\). Tìm giá trị của x và y để biểu thức P=\(\left(x^4+1\right)\left(y^4+1\right)\) đạt giá trị nhỏ nhất. Tìm giá trị nhỏ nhất ấy.
TK: Tìm Min (x^4 + 1) (y^4 + 1) với x + y = căn10 ; x , y > 0 - Thanh Truc
Đúng 0
Bình luận (0)
Cho biểu thức hai biến: \(f\left(x,y\right)=\left(2x-3y+7\right)\left(3x+2y-1\right)\)
a, Tìm các giá trị của y sao cho phương trình ( ẩn x) f(x,y)=0 nhận x=-3 làm nghiệm
b, Tìm các giá trị của x sao cho phương trình ( ẩn y) f(x,y)=0 nhận y=2 làm nghiệm
a, Phương trình f(x,y) =0 <=> (2x-3y+7)(3x+2y-1) =0 nhận x=-3 làm nghiệm nên ta có:(-6-3y +7)(-9 + 2y -1)=0
<=> (1 - 3y)(2y - 10) =0 <=> 1 - 3y=0 hoặc 2y - 10 =0
* 1-3y=0 <=> y=1/3
* 2y - 10= 0 <=> y=5
vậy phương trình nhận x=-3 thì y=1/3 hoặc y=5
b, Phương trình nhận y=2 làm nghiệm nên ta có:
(2x - 6 + 7)(3x+ 4 - 1)=0
<=> (2x + 1)(3x + 3) =0 <=> 2x + 1=0 hoặc 3x + 3 = 0
<=> x=-1/ 2 hoặc x=-1
vậy phương trình nhận y=2 làm nghiệm thì x=-1/2 hoặc x=-1
Đúng 0
Bình luận (0)
a, Phương trình f(x,y) =0 <=> (2x-3y+7)(3x+2y-1) =0 nhận x=-3 làm nghiệm nên ta có:(-6-3y +7)(-9 + 2y -1)=0
<=> (1 - 3y)(2y - 10) =0 <=> 1 - 3y=0 hoặc 2y - 10 =0
* 1-3y=0 <=> y=1/3
* 2y - 10= 0 <=> y=5
vậy phương trình nhận x=-3 thì y=1/3 hoặc y=5
b, Phương trình nhận y=2 làm nghiệm nên ta có:
(2x - 6 + 7)(3x+ 4 - 1)=0
<=> (2x + 1)(3x + 3) =0 <=> 2x + 1=0 hoặc 3x + 3 = 0
<=> x=-1/ 2 hoặc x=-1
vậy phương trình nhận y=2 làm nghiệm thì x=-1/2 hoặc x=-1
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất của biểu thức sau, biết x và y ;à các số thực dương :
\(A=\frac{\left(x+y+1\right)^2}{xy+x+y}+\frac{xy+x+y}{\left(x+y+1\right)^2}\)
dự đoán của chúa Pain x=y=1
áp dụng BDT cô si ta có
\(A\ge2\sqrt{\frac{\left(x+y+1\right)^2.\left(xy+x+y\right)}{\left(xy+x+y\right)\left(x+y+1\right)^2}}=2.\)
dấu = xảy ra khi
\(\left(x+y+1\right)^2=xy+x+y\) :)
Đúng 0
Bình luận (0)
Tính giá trị của biểu thức: \(E=x\sqrt{1+y^2}+y\sqrt{1+x^2}\), biết \(xy+\sqrt{\left(1+x^2\right).\left(1+y^2\right)}=a\)
Tính giá trị của biểu thức: \(E=x\sqrt{1+y^2}+y\sqrt{1+x^2}\) biết \(xy+\sqrt{\left(1+x^2\right).\left(1+y^2\right)}=a\)
\(xy+\sqrt{\left(1+x^2\right)\left(1+y^2\right)}=a\)
\(\Rightarrow x^2y^2+2xy\sqrt{\left(1+x^2\right)\left(1+y^2\right)}+\left(1+x^2\right)\left(1+y^2\right)=a^2\)
\(\Rightarrow x^2\left(1+y^2\right)+y^2\left(1+x^2\right)+2.x\sqrt{1+y^2}.y\sqrt{1+x^2}+1=a^2\)
\(\Rightarrow\left(x\sqrt{1+y^2}+y\sqrt{1+x^2}\right)^2+1=a^2\)
\(\Rightarrow E^2+1=a^2\)
\(\Rightarrow E=\pm\sqrt{a^2-1}\)
Đúng 6
Bình luận (0)
\(a^2=x^2y^2+(1+x^2)(1+y^2)+2xy\sqrt{(1+x^2)(1+y^2)} \\->2xy\sqrt{(1+x^2)(1+y^2)}=a^2-2x^2y^2-1-x^2-y^2 \\E^2=x^2(1+y^2)+y^2(1+x^2)+2xy\sqrt{(1+x^2)(1+y^2)} \\=x^2+y^2+2x^2y^2+a^2-2x^2y^2-1-x^2-y^2 \\=a^2-1\)
Đúng 2
Bình luận (0)
Tính giá trị của biểu thức: \(E=x\sqrt{1+y^2}+y\sqrt{1+x^2}\), biết \(xy+\sqrt{\left(1+x^2\right).\left(1+y^2\right)}=a\)
\(E^2=x^2\left(y^2+1\right)+y^2\left(x^2+1\right)+2xy\sqrt{\left(y^2+1\right)\left(x^2+1\right)}\)
\(=2\left(xy\right)^2+x^2+y^2+2xy\sqrt{\left(x^2+1\right)\left(y^2+1\right)}\)
\(a^2=\left(xy\right)^2+2xy\sqrt{\left(x^2+1\right)\left(y^2+1\right)}+\left(x^2+1\right)\left(y^2+1\right)\)
\(=2\left(xy\right)^2+2xy\sqrt{\left(x^2+1\right)\left(y^2+1\right)}+x^2+y^2+1\)
\(\Rightarrow E^2=a^2-1\Rightarrow E=\sqrt{a^2-1}\)
Đúng 2
Bình luận (0)
\(E=x\sqrt{1+y^2}+y\sqrt{1+x^2}\)
\(\Leftrightarrow E^2=x^2\left(1+y^2\right)+y^2\left(1+x^2\right)+2xy\sqrt{\left(1+y^2\right)\left(1+x^2\right)}\)
\(=2x^2y^2+x^2+y^2+2xy\left(a-xy\right)\)
\(=2x^2y^2+x^2+y^2+2xya-2x^2y^2\)
\(=x^2+y^2+2xya\)
\(=\left(2xy\right)2+a=a^2+a=E^2\)
\(E=\sqrt{a^2+a}\)
Đúng 1
Bình luận (0)
\(\rightarrow E^2=x^2\left(1+y^2\right)+y^2\left(1+x^2\right)+\\ 2xy\sqrt{\left(1+y^2\right)\left(1+x^2\right)}\\ =2xy^2+x^2+y^2+2xy\left(a-xy\right)\\ =2x^2y^2+x^2+y^2+2xya-2x^2y^2\\ =x^2+y^2+2xya\\ =\left(x+y\right)^2+a=a^2+a\\ =E^2\\ Vậy.E=\sqrt{a^2+a}\)
Đúng 2
Bình luận (1)