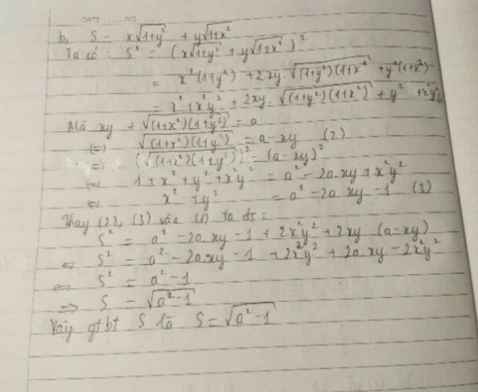Violympic toán 9
Các câu hỏi tương tự
Tính giá trị của biểu thức: \(E=x\sqrt{1+y^2}+y\sqrt{1+x^2}\) biết \(xy+\sqrt{\left(1+x^2\right).\left(1+y^2\right)}=a\)
Tính giá trị của biểu thức: \(E=x\sqrt{1+y^2}+y\sqrt{1+x^2}\), biết \(xy+\sqrt{\left(1+x^2\right).\left(1+y^2\right)}=a\)
Cho xy + \(\sqrt{\left(1+x^2\right)\left(1+y^2\right)}\) = 20122011
Hãy tính giá trị biểu thức M = x\(\sqrt{1+y^2}\) + y\(\sqrt{1+x^2}\)
tìm x,y,z để biểu thức sau có giá trị bằng 2
\(A=\dfrac{x}{\left(\sqrt{x}+\sqrt{y}\right)\left(1-\sqrt{y}\right)}-\dfrac{y}{\left(\sqrt{x}+\sqrt{y}\right)\left(\sqrt{x}+1\right)}-\dfrac{xy}{\left(1+\sqrt{x}\right)\left(1-\sqrt{y}\right)}\)
Cho các số x,y thỏa mãn: \(\left(x+\sqrt{3+x^2}\right).\left(y+\sqrt{3+y^2}\right)=3\). Tính giá trị của biểu thức: \(A=4x^2+xy+y^2+15\)
Cho các số x,y thỏa mãn: \(\left(x+\sqrt{3+x^2}\right).\left(y+\sqrt{3+y^2}\right)=3\). Tính giá trị của biểu thức: \(A=4x^4+xy+y^2+15\)
cho biểu thức
\(P=\left(\dfrac{\sqrt{x}+\sqrt{y}}{1-\sqrt{xy}}+\dfrac{\sqrt{x}-\sqrt{y}}{1+\sqrt{xy}}\right):\left(1+\dfrac{x+y+2xy}{1-xy}\right)\)
a) rút gọn biểu thức P
b)tính giá trị của biểu thức P với x=\(\dfrac{2}{2+\sqrt{3}}\)
tính giá trị của biểu thức \(A=\left(x-y\right)^3+3\left(x-y\right)\left(xy+1\right)\) biết rằng \(x=\sqrt[3]{2+\sqrt{3}}-\sqrt[3]{2-\sqrt{3}}\), \(y=\sqrt[3]{\sqrt{5}+2}-\sqrt[3]{\sqrt{5}-2}\)
Rút gọn biểu thức:
\(P=\left(\dfrac{1}{xy\sqrt{y}}-\dfrac{1}{xy\sqrt{x}}\right):\left(\dfrac{1}{x^2+xy+2x\sqrt{xy}}+\dfrac{1}{xy+y^2+2y\sqrt{xy}}+\dfrac{2}{\sqrt{xy}\left(\sqrt{x}+\sqrt{y}\right)^2}\right)\)